Тригонометрия

Пи

const float pi = 3.14159265f; // на самом деле бесконечное число цифр

Косинус и синус

(Источник: http://commons.wikimedia.org/wiki/User:Geek3 , под лицензией GNU Free Documentation License )

Единичная окружность

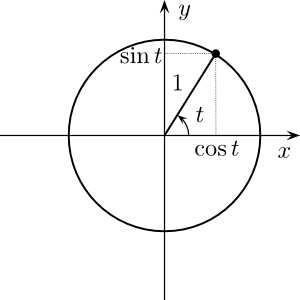
( Изменено на основе http://en.wikipedia.org/wiki/User:Gustavb под лицензией Crative Commons 3.0 ) t - угол в радианах.

0 радиан = 0 градусов

180 градусов = Pi радиан

360 градусов ( полный круг ) = 2*Pi радиан

90 градусов = Pi/2 радиан

Вектора

ВСЕГДА необходимо знать в каких координатах ваш вектор. Подробнее смотрите в разделе 3.

Однородные координаты

Трёхмерный вектор представляется как (x,y,z), но однородный трёхмерный вектор - (x,y,z,w).

• w=0 : это направление
• w=1 : это позиция
• иначе : все еще может быть допустимым, но вам лучше знать, что вы делаете.

Вы можете только перемножать матрицу 4x4 с однородным вектором.

Длина

Как и декартово растояние: sqrt( x² + y² + z² ). w не учитывается.

Векторное произведение

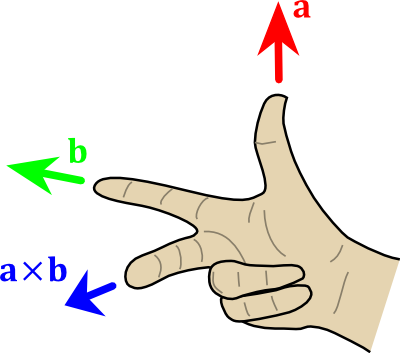
( Изменено на основе http://en.wikipedia.org/wiki/User:Acdx , прежнее изображение под лицензией Creative Commons 3.0 )

X обозначет вектороное произведение. длина( a x b ) == длина(a) * длина(b) * sin(θ), поэтому вы можете нормализовать (normalize()) результат.

Скалярное произведение

##

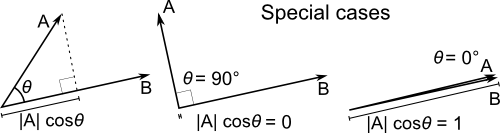
( Источник: http://en.wikipedia.org/wiki/File:Dot_Product.svg ) A.B = длина(A)cos(Theta) , но, скорее всего, вычисляется как A.xB.x +A.yB.y +A.zB.z

Сложение и вычитание

покомпонентно :

res.x = A.x + B.x
res.y = A.y + B.y
...

Multiplication

покомпонентно :

res.x = A.x * B.x
res.y = A.y * B.y
...

Нормализация

Разделите вектор на его длину:

normalizedVector = vec * ( 1.0f / vec.length() )

Матрицы

Умножение Матрица-Матрица

пример для матрицы переноса:

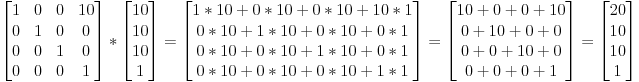
Умножение Матрица-Вектор

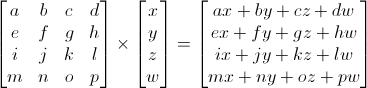
Обычные преобразования

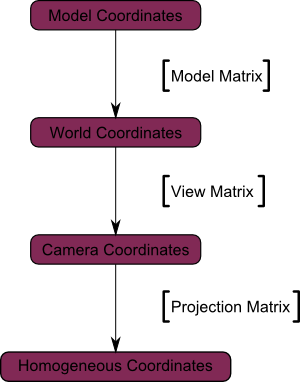
… но в ваших шейдерах вы также можете представлять свои векторы в касательном пространстве. И в пространстве изображений, когда вы делаете пост-эффекты.

res.x = A.x + B.x