Движок не перемещает корабль. Корабль остается на месте, а движок перемещает вселенную относительно его.

Futurama

Это очень важная часть уроков, убедитесь что прочитали ее несколько раз и хорошо поняли.

Однородные координаты

До текущего момента мы оперировали 3х-мерными вершинами как (x, y, z) триплетами. Введем еще один параметр w и будем оперировать векторами вида (x, y, z, w).

Запомните навсегда, что:

• Если w == 1, то вектор (x, y, z, 1) - это позиция в пространстве.
• Если же w == 0, то вектор (x, y, z, 0) - это направление.

Что это дает нам? Ок, для поворота это ничего не меняет, так как и в случае поворота точки и в случае поворота вектора направления вы получаете один и тот же результат. Однако в случае переноса есть разница. Перенос вектора направления даст тот же самый вектор. Подробнее об этом остановимся позднее.

Однородные координаты позволяют нам с помощью одной математической формулы оперировать векторами в обоих случаях.

Матрицы трансформаций

Введение в матрицы

Проще всего представить матрицу, как массив чисел, со строго определенным количеством строк и столбцов. К примеру, матрица 2x3 выглядит так:

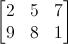
Однако в трехмерной графике мы будем использовать только матрицы 4x4, которые позволят нам трансформировать наши вершины (x, y, z, w). Трансформированная вершина является результатом умножения матрицы на саму вершину:

Матрица x Вершина (именно в этом порядке!!) = Трансформир. вершина

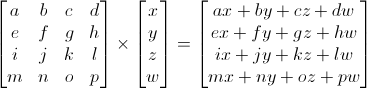
Довольно просто. Мы будем использовать это довольно часто, так что имеет смысл поручить это компьютеру:

В C++, используя GLM:

glm::mat4 myMatrix;
glm::vec4 myVector;
// Не забудьте тут заполнить матрицу и вектор необходимыми значениями
glm::vec4 transformedVector = myMatrix * myVector; // Обратите внимание на порядок! Он важен!

В GLSL :

mat4 myMatrix;
vec4 myVector;
// Не забудьте тут заполнить матрицу и вектор необходимыми значениями
vec4 transformedVector = myMatrix * myVector; // Да, это очень похоже на GLM :)

Попробуйте поэкспериментировать с этими фрагментами.

Матрица переноса

Матрица переноса выглядит так:

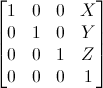
где X, Y, Z - это значения, которые мы хотим добавить к нашему вектору.

Значит, если мы захотим перенести вектор (10, 10, 10, 1) на 10 юнитов в направлении X, то мы получим:

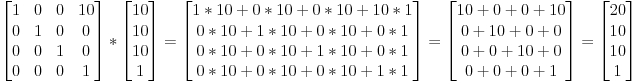
… получим (20, 10, 10, 1) однородный вектор! Не забывайте, что 1 в параметре w, означает позицию, а не направление и наша трансформация не изменила того, что мы работаем с позицией.

Теперь посмотрим, что случится, если вектор (0, 0, -1, 0) представляет собой направление:

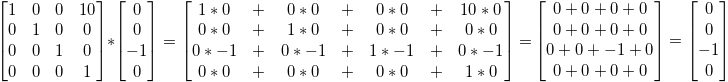
… и получаем наш оригинальный вектор (0, 0, -1, 0). Как было сказано раньше, вектор с параметром w = 0 нельзя перенести.

И самое время перенести это в код.

В C++, с GLM:

#include <glm/gtc/transform.hpp> // после <glm/glm.hpp>

glm::mat4 myMatrix = glm::translate(glm::mat4(), glm::vec3(10.0f, 0.0f, 0.0f));
glm::vec4 myVector(10.0f, 10.0f, 10.0f, 0.0f);
glm::vec4 transformedVector = myMatrix * myVector;

В GLSL:

vec4 transformedVector = myMatrix * myVector;

По факту, вы никогда не будете делать это в шейдере, чаще всего вы будете выполнять glm::translate() в C++, чтобы вычислить матрицу, передать ее в GLSL, а уже в шейдере выполнить умножение

Единичная матрица

Это специальная матрица, которая не делает ничего, но мы затрагиваем ее, так как важно помнить, что A умноженное на 1.0 дает A:

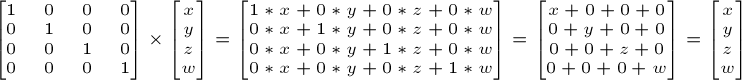
В C++ :

glm::mat4 myIdentityMatrix = glm::mat4(1.0f);

Матрица масштабирования

Выглядит также просто:

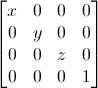
Значит, если вы хотите применить масштабирование вектора (позицию или направление - это не важно) на 2.0 во всех направлениях, то вам необходимо:

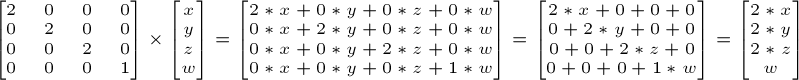
Обратите внимание, что w не меняется, а также обратите внимание на то, что единичная матрица - это частный случай матрицы масштабирования с коэффициентом масштаба равным 1 по всем осям. Также единичная матрица - это частный случай матрицы переноса, где (X, Y, Z) = (0, 0, 0) соответственно.

В C++ :

// добавьте #include <glm/gtc/matrix_transform.hpp> и #include <glm/gtx/transform.hpp>
glm::mat4 myScalingMatrix = glm::scale(2.0f, 2.0f ,2.0f);

Матрица поворота

Сложнее чем рассмотренные ранее. Мы опустим здесь детали, так как вам не обязательно знать это точно для ежедневного использования. Для получения более подробной информации можете перейти по ссылке Matrices and Quaternions FAQ (довольно популярный ресурс и возможно там доступен ваш язык)

В C++ :

// добавьте #include <glm/gtc/matrix_transform.hpp> и #include <glm/gtx/transform.hpp>
glm::vec3 myRotationAxis( ??, ??, ??);
glm::rotate( angle_in_degrees, myRotationAxis );

Собираем трансформации вместе

Итак, теперь мы умеем поворачивать, переносить и масштабировать наши векторы. Следующий шагом было бы неплохо объединить трансформации, что реализуется по следующей формуле:

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;

ВНИМАНИЕ! Эта формула на самом деле показывает, что сначала выполняется масштабирование, потом поворот и только в самую последнюю очередь выполняется перенос. Именно так работает перемножение матриц.

Обязательно запомните в каком порядке все это выполняется, потому что порядок действительно важен, в конце концов вы можете сами это проверить:

• Сделайте шаг вперед и повернитесь влево
• Повернитесь влево и сделайте шаг вперед

Разницу действительно важно понимать, так как вы постоянно будете с этим сталкиваться. К примеру, когда вы будете работать с игровыми персонажами или какими-то объектами, то всегда сначала выполняйте масштабирование, потом поворот и только потом перенос.

На самом деле, приведенный выше порядок - это то, что вам обычно нужно для игровых персонажей и других предметов: сначала масштабируйте его, если это необходимо; затем установливаете его направление, а затем перемещаете его. Например, для модели судна (повороты удалены для упрощения):

• Неправильный путь :
  • Вы переносите корабль на (10, 0, 0). Его центр теперь находится в 10 единицах от начала координат.
  • Вы масштабируете свой корабль в 2 раза. Каждая координата умножается на 2 “относительно исходной”, что далеко… Итак, вы попадаете в большой корабль, но его центр 2 * 10 = 20. Не то, что вы хотели.
• Правильный путь :
  • Вы масштабируете свой корабль в 2 раза. Вы получаете большой корабль, с центром в начале координат.
  • Вы переносите свой корабль. Он по прежнему того же размера и на правильном расстоянии.

Перемножение двух матриц очень похоже на перемножение матрицы и вектора, поэтому мы опустим описание, а если вы хотите узнать больше, то можете опять перейти по ссылке Matrices and Quaternions FAQ.

В C++, с GLM :

glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;

В GLSL :

mat4 transform = mat2 * mat1;
vec4 out_vec = transform * in_vec;

Мировая, видовая и проекционная матрицы

До конца этого урока мы будем полагать, что знаем как отображать любимую 3D модель из Blender - обезьянку Suzanne.

Мировая, видовая и проекционная матрицы - это удобный инструмент для разделения трансформаций.

Мировая матрица

Эта модель, также, как и наш красный треугольник задается множеством вершин, координаты которых заданы относительно центра объекта, т. е. вершина с координатами (0, 0, 0) будет находиться в центре объекта.

Далее мы бы хотели перемещать нашу модель, так как игрок управляет ей с помощью клавиатуры и мышки. Все, что мы делаем - это применяем масштабирование, потом поворот и перенос. Эти действия выполняются для каждой вершины, в каждом кадре (выполняются в GLSL, а не в C++!) и тем самым наша модель перемещается на экране.

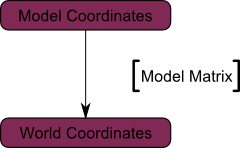
Теперь наши вершины в мировом пространстве. Это показывает черная стрелка на рисунке. Мы перешли из пространства объекта (все вершины заданы относительно центра объекта) к мировому пространству (все вершины заданы относительно центра мира).

Схематично это показывается так:

Видовая матрица

Еще раз процитируем Футураму:

Движок не перемещает корабль. Корабль остается на том же месте, а движок перемещает вселенную вокруг него.

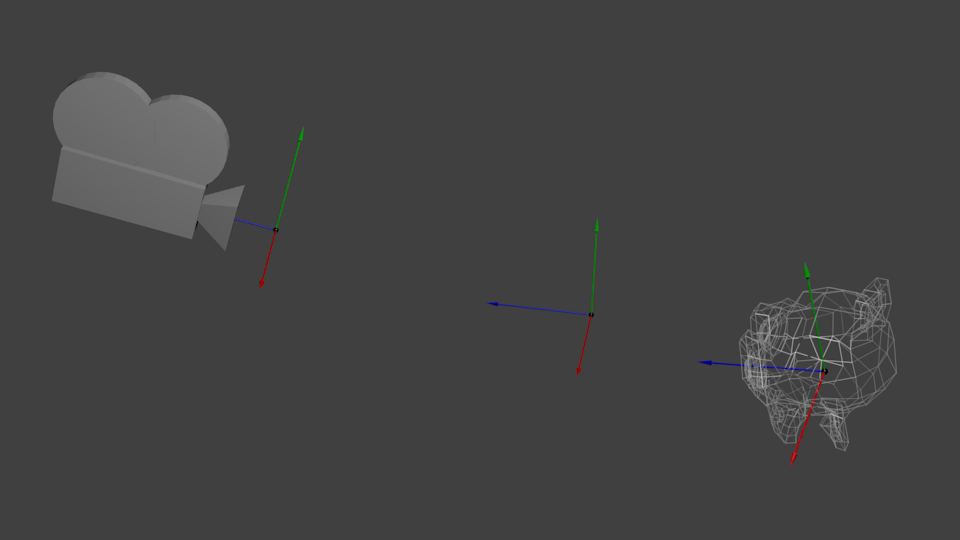
Попробуйте представить это применительно к камере. Например, если вы хотите сфотографировать гору, то вы не перемещаете камеру, а перемещаете гору. Это не возможно в реальной жизни, но это невероятно просто в компьютерной графике.

Итак, изначально ваша камера находится в центре мировой системы координат. Чтобы переместить мир вам необходимо ввести еще одну матрицу. Допустим, что вы хотите переместить камеру на 3 юнита ВПРАВО (+X), что будет эквивалентом перемещения всего мира на 3 юнита ВЛЕВО (-X). В коде это выглядит так:

// Добавьте #include <glm/gtc/matrix_transform.hpp> и #include <glm/gtx/transform.hpp>
glm::mat4 ViewMatrix = glm::translate(glm::mat4(), glm::vec3(-3.0f, 0.0f, 0.0f));

Опять же, изображение ниже полностью показывает это. Мы перешли из мировой системы координат (все вершины заданы относительно центра мировой системы) к системе координат камеры (все вершины заданы относительно камеры):

И пока ваш мозг переваривает это, мы посмотрим на функцию, которую предоставляет нам GLM, а точнее на glm::LookAt:

glm::mat4 CameraMatrix = glm::LookAt(
    cameraPosition, // Позиция камеры в мировом пространстве
    cameraTarget,   // Указывает куда вы смотрите в мировом пространстве
    upVector        // Вектор, указывающий направление вверх. Обычно (0, 1, 0)
);

А вот диаграмма, которая показывает то, что мы делаем:

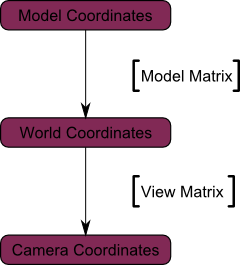
Однако это еще не конец.

Проекционная матрица

Итак, теперь мы находимся в пространстве камеры. Это означает, что вершина, которая получит координаты x == 0 и y == 0 будет отображаться по центру экрана. Однако, при отображении объекта огромную роль играет также дистанция до камеры (z). Для двух вершин, с одинаковыми x и y, вершина имеющая большее значение по z будет отображаться ближе, чем другая.

Это называется перспективной проекцией:

И к счастью для нас, матрица 4х4 может выполнить эту проекцию¹:

// Создает действительно трудночитаемую матрицу, но, тем не менее это стандартная матрица 4x4
glm::mat4 projectionMatrix = glm::perspective(
    glm::radians(FoV), // Вертикальное поле зрения в радианах. Обычно между 90° (очень широкое) и 30° (узкое)
    4.0f / 3.0f,       // Отношение сторон. Зависит от размеров вашего окна. Заметьте, что 4/3 == 800/600 == 1280/960
    0.1f,              // Ближняя плоскость отсечения. Должна быть больше 0.
    100.0f             // Дальняя плоскость отсечения.
);

Еще раз:

Мы перешли из Пространства Камеры (все вершины заданы относительно камеры) в Однородное пространство (все вершины находятся в небольшом кубе. Все, что находится внутри куба - выводится на экран).

Схема:

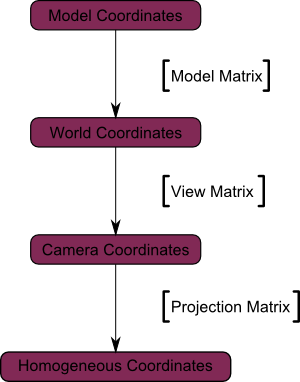
Теперь посмотрим на следующие изображения, чтобы вы могли лучше понять что же происходит с проекцией. До проецирования мы имеем синие объекты в пространстве камеры, в то время как красная фигура показывает обзор камеры, т. е. все то, что видит камера.

Применение Проекционной матрицы дает следующий эффект:

На этом изображении обзор камеры представляет собой куб и все объекты деформируются. Объекты, которые находятся ближе к камере отображаются большими, а те, которые дальше - маленькими. Прямо как в реальности!

Вот так это будет выглядеть:

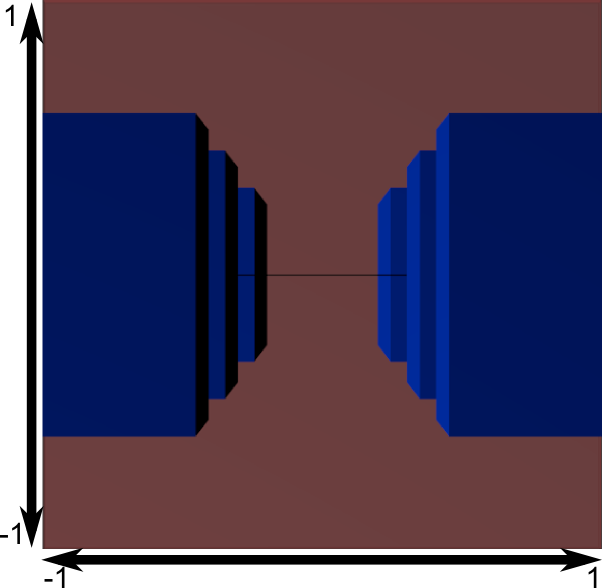
Изображение является квадратным, поэтому следующие математические трансформации применяются, чтобы растянуть изображение согласно актуальным размерам окна:

И это изображение является тем, что на самом деле будет выведено.

Объединяем трансформации : матрица ModelViewProjection

… Просто стандартные матричные преобразования, которые вы уже полюбили!

// C++ : вычисление матрицы
glm::mat4 MVPmatrix = projection * view * model; // Запомните! В обратном порядке!

// GLSL : применение матрицы
transformed_vertex = MVP * in_vertex;

Совмещаем все вместе

• Первый шаг - создание нашей MVP матрицы. Это должно быть сделано для каждой модели, которую вы отображаете.

// Проекционная матрица : 45&deg; поле обзора, 4:3 соотношение сторон, диапазон : 0.1 юнит <-> 100 юнитов
glm::mat4 Projection = glm::perspective(glm::radians(45.0f), 4.0f / 3.0f, 0.1f, 100.0f);

// Или, для ортокамеры
glm::mat4 View       = glm::lookAt(
    glm::vec3(4,3,3), // Камера находится в мировых координатах (4,3,3)
    glm::vec3(0,0,0), // И направлена в начало координат
    glm::vec3(0,1,0)  // "Голова" находится сверху
);
// Матрица модели : единичная матрица (Модель находится в начале координат)
glm::mat4 Model = glm::mat4(1.0f);  // Индивидуально для каждой модели

// Итоговая матрица ModelViewProjection, которая является результатом перемножения наших трех матриц
glm::mat4 MVP = Projection * View * Model; // Помните, что умножение матрицы производиться в обратном порядке

• Второй шаг - передать это в GLSL:

// Получить хэндл переменной в шейдере
// Только один раз во время инициализации.
GLuint MatrixID = glGetUniformLocation(programID, "MVP");

// Передать наши трансформации в текущий шейдер
// Это делается в основном цикле, поскольку каждая модель будет иметь другую MVP-матрицу (как минимум часть M)
glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &MVP[0][0]);

• Третий шаг - используем полученные данные в GLSL, чтобы трансформировать наши вершины.

  // Входные данные вершин, разные для всех исполнений этого шейдера.
  layout(location = 0) in vec3 vertexPosition_modelspace;
  
  // Значения, которые остаются постоянными для всей сетки.
  uniform mat4 MVP;
  
  void main(){
    // Выходная позиция нашей вершины: MVP * position
    gl_Position =  MVP * vec4(vertexPosition_modelspace,1);
  }

• Готово! Теперь у нас есть такой же треугольник как и в Уроке 2, все так же находящийся в начале координат (0, 0, 0), но теперь мы его видим в перспективе из точки (4, 3, 3).

В Уроке 6 вы научитесь изменять эти значения динамически, используя клавиатуру и мышь, чтобы создать камеру, которую вы привыкли видеть в играх. Но для начала мы узнаем как придать нашем моделям цвета (Урок 4) и текстуры (Урок 5).

Задания

• Попробуйте поменять значения glm::perspective
• Вместо использования перспективной проекции попробуйте использовать ортогональную (glm:ortho)
• Измените ModelMatrix для перемещения, поворота и масштабирования треугольника
• Используйте предыдущее задание, но с разным порядком операций. Обратите внимание на результат.

Замечания