Billboards
빌보드는 3D공간에서 표현되는 2D 요소다. 화면 내 모든 것을 가리는 2D메뉴 같은 것도 아니고 회전 시키는 3D 평면도 아니다. 대부분의 게임에서 체력바를 표시할 때 사용하는 것이라고 생각하면 된다.
빌보드가 다른 요소들과 다른 점은 공간에서 위치를 가지되 회전은 자동으로 계산되어 항상 카메라를 바라보게 만든다는 점이다.
솔루션 #1 : 2D 방식
이 방법은 매우 쉽다. 단순히 화면 내 위치를 계산하고, 이 위치에 2D 텍스트를 표시한다.(튜토리얼 11을 참고)
// 여기에서 설명한 모든 것들은 튜토리얼 3을 참고하도록 하자!
// 새로운 것은 전혀 없다.
glm::vec4 BillboardPos_worldspace(x,y,z, 1.0f);
glm::vec4 BillboardPos_screenspace = ProjectionMatrix * ViewMatrix * BillboardPos_worldspace;
BillboardPos_screenspace /= BillboardPos_screenspace.w;
if (BillboardPos_screenspace.z < 0.0f){
// 오브젝트가 카메라 뒤쪽에 있다면, 표시하지 않는다.
}
짜잔~! 이 방법의 좋은 점은 매우 쉽다는 점이며 카메라의 거리에 상관없이 항상 같은 크기를 가진다. 하지만 2D 텍스트는 다른 요소들보다 무조건 위쪽에 나타나며 경우에 따라 다른 오브젝트를 위쪽에 표시하고 싶을 때 문제가 될 수 있다.
솔루션 #2 : 3D 방식
이 방법이 보통 더 괜찮고 생각보다 복잡하지 않다. 목표는 메시를 카메라에 정렬하는 것이다. 비록 카메라가 움직인다고 하더라도.

이 문제는 적절한 모델 행렬(Model Matrix)을 생성하는 것이라고 생각하면 된다. 기본적인 아이디어는 빌보드의 각 코너 부분을 센터 포지션을 기준으로 카메라의 Up, Right 벡터를 사용해 표시하는 것이다.
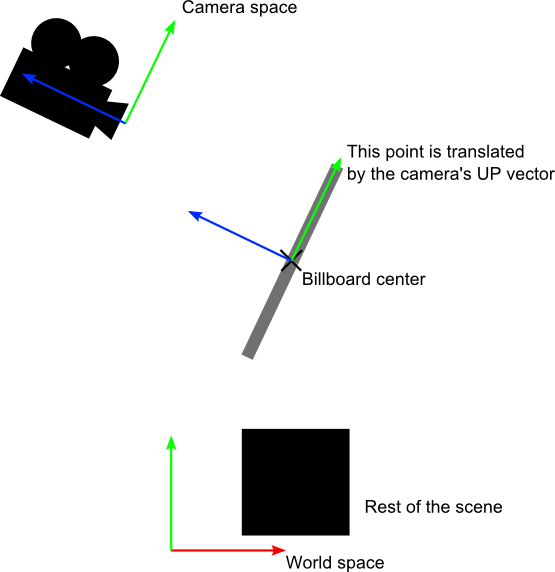
현재 우리가 알고 있는 것은 월드 공간에서의 빌보드의 센터 포지션과 카메라의 Up, Right 벡터다.
카메라 공간에서 카메라의 Up 벡터의 값은 (0,1,0)이다. 월드 공간에서 값을 얻으려면 카메라 공간 -> 월드 공간 행렬을 곱하면 된다. 그리고 이 행렬은 뷰 행렬(View Matrix)의 역행렬이다. 간단하게 수학적으로 표현하면 다음과 같다.
CameraRight_worldspace = {ViewMatrix[0][0], ViewMatrix[1][0], ViewMatrix[2][0]}
CameraUp_worldspace = {ViewMatrix[0][1], ViewMatrix[1][1], ViewMatrix[2][1]}
이제 최종적으로 버텍스의 포지션을 계산하는 것은 매우 쉽다.
vec3 vertexPosition_worldspace =
particleCenter_wordspace
+ CameraRight_worldspace * squareVertices.x * BillboardSize.x
+ CameraUp_worldspace * squareVertices.y * BillboardSize.y;
- particleCenter_worldspace는 이름에서 알 수 있듯이 빌보드의 센터 포지션이다. 이것은 uniform vec3로 지정되어 있다.
- squareVertices는 오리지널 메시다. 왼쪽 버텍스의 squareVertices.x는 -0.5로 설정되어 있으며 카메라의 왼쪽을 의미한다.(이 값에 CameraRight_worldspace를 곱 하는걸 눈여겨 보자.)
- BillboardSize는 빌보드의 크기이며 단위는 월드 단위다. 이것 역시 uniform으로 지정되어 있다.

실제 squareVertices는 아래와 같이 만들어 진다.
// VBO는 파티클의 4개 버텍스를 가지고 있다.
static const GLfloat g_vertex_buffer_data[] = {
-0.5f, -0.5f, 0.0f,
0.5f, -0.5f, 0.0f,
-0.5f, 0.5f, 0.0f,
0.5f, 0.5f, 0.0f,
};
솔루션 #3 : 고정 사이즈 3D 방식
앞서 보았듯이 빌보드의 사이즈는 카메라의 거리에 따라 바뀐다. 물론 이렇게 변화하는 것이 의도에 맞는 결과일 수도 있지만 체력 바와 같은 경우에 카메라 거리에 상관없이 고정된 크기로 나오길 원할 수도 있다. 지금은 센터와 코너의 위치가 스크린 공간에서 고정되길 원하므로 센터 포지션과 오프셋을 스크린 공간에서 계산하도록 하자.
vertexPosition_worldspace = particleCenter_wordspace;
// 스크린 공간의 파티클 센터 포지션을 얻는다.
gl_Position = VP * vec4(vertexPosition_worldspace, 1.0f);
// 원근 나누기(Perspective division)를 우리가 직접 해야만 한다.
gl_Position /= gl_Position.w;
// 버텍스를 스크린 공간에서 직접 욺직인다. Camera의 월드 공간에서 Up/Right를 필요하지 않다.
gl_Position.xy += squareVertices.xy * vec2(0.2, 0.05);
기억할 것은 지금 렌더링 파이프라인의 스테이지가 NDC(Normalized Device Coordinates)라는 것이다. 그러므로 값의 범위는 -1 ~ 1이 된다. (픽셀이 아니다.) 픽셀 단위에서의 크기를 알고 싶다면 BillboardSizeInScreenPercentage를 사용하지 말고 (ScreenSizeInPixels / BillboardSizeInPixels)를 사용하면 된다.

솔루션 #4 : 수직 회전만
일부 시스템 모델에서 나무 혹은 램프는 수직축을 기준으로만 회전할 수도 있다. 하나의 축을 기준으로만 회전하는 하이브리드 시스템이 필요할 수도 있는데 이것은 독자 여러분들의 숙제로 남겨두겠다!