8번째 튜토리얼에선, 이제 어떻게 기초적인 쉐이딩을 하는지 배울거에요. 아래 내용을 포함해요:

광원에 가까워질 때 더 밝아지는 법.
빛의 반사로 하이라이트를 만드는 법. (Specular Lighting - 반사 조명)
빛이 모델을 직접 향하지 않아도 빛이 보이는 법. (Diffuse Lighting - 기본 조명)
개쩌는 속임수. (ambient Lighting)

아래는 포함하지 않아요 :

그림자. 이건 따로 튜토리얼을 만들어야 할 정도로 광대한 주제에요.
거울 같은 반사 (물 포함해서.)
표면이 산란하는 것 같은 정됴한 빛 - 물질 상호 작용 (왁스같이 번쩍 번쩍.)
이방성 표면 (잘 닦은 금속과 같은. )
물리 기반 셰이딩, 현실과 비슷한.
주변 폐색하기 (역주 : 빛이 안 들어오는 곳에 안 들어오게 하는 거.)(동굴에서 더 어두워 짐.)
색상 번지게 하기. (레드 카펫이 하얀 천장을 붉게 만듭니다. )
투명도
모든 종류의 글로벌 일루미네이션(GI) (더럽게 어려워!)

한 마디로 : 기초죠.

법선 벡터(normals)

지금까지 튜로리얼에서 normal을 소개를 못 드렸어요. 드디어 오늘 소개 드릴게요!

삼각형 법선

평면의 법선이란, 길이가 1이고 평면에 수직인 벡터를 말해요.

삼각형의 법선은 그럼 길이가 1이고, 삼각형에 수직인 백터를 말하겠죠? 이건 가장자리에 있는 두 벡터를 외적(외적은 a,b 두 백터의 수직 백터를 구하는 작업이었죠. 기억하시죠? )함으로써 쉽게 구할 수 있고, 일반화 시킬 수도 있죠 : 일반화는, 길이를 1로 만드는 작업을 말해요. 의사코드를 보죠!:

triangle ( v1, v2, v3 )
edge1 = v2-v1
edge2 = v3-v1
triangle.normal = cross(edge1, edge2).normalize()

normal과 normalize()를 햇갈리지 마세요. Normailize()는 새 길이가 1이 되도록 벡터를 길이로 나누는 작업이에요. normal은 그 백터를 표현할 수 있는 이름이에요. 음. normal말이에요.

정점의 법선들

확장하면, 정점의 법선은 주위 삼각형의 법선의 조합이라고 할 수 있어요. Vertex Shader는 앞서 말한 삼각형은 다루지 않고, 정점들을 다루니까 그렇게 말하는 게 더 편할거에요. 어차피 OpenGL에서는 삼각형들에 대한 정보를 얻을 길이 없으니까요. 의사 코드에요 :

vertex v1, v2, v3, ....
triangle tr1, tr2, tr3 // all share vertex v1
v1.normal = normalize( tr1.normal + tr2.normal + tr3.normal )

OpenGL에서 정점의 법선을 사용하기.

OpenGL에서 법선을 쓰는 건, 아주 쉬워요! 법선은 정점의 속성이에요. 마치 위치나, 색상이나, UV 좌표 같은 것들 말이에요. 그러니까 해온 대로 합시다. 이미 우리의 loadOBJ 파일에서는 OBJ 파일을 읽으면서 모든 준비를 맞춘 것 같네요.

GLuint normalbuffer;
 glGenBuffers(1, &normalbuffer);
 glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
 glBufferData(GL_ARRAY_BUFFER, normals.size() * sizeof(glm::vec3), &normals[0], GL_STATIC_DRAW);

and

 // 3번째 버퍼의 속성 : 법선들
 glEnableVertexAttribArray(2);
 glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
 glVertexAttribPointer(
     2,                                // attribute
     3,                                // size
     GL_FLOAT,                         // type
     GL_FALSE,                         // normalized?
     0,                                // stride
     (void*)0                          // array buffer offset
 );

자. 이제 시작하기는 충분해 보여요.

Diffuse 부분

표면 법선의 중요성

빛이 물체에 닿을 때, 중요한 점은 모든 방향으로 반사된다는 점이에요. 그걸 “확산 요소”라고 불러요. (곧 있으면 도대체 무슨 일이 벌어지는 지 알 수 있을거에요.)

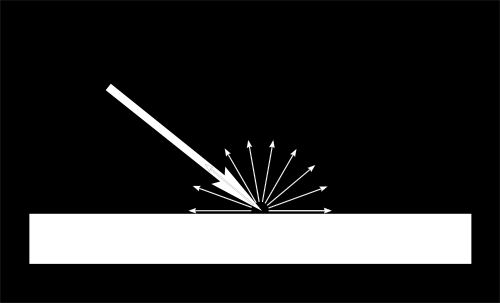
어떤 빛이 표면에 도달하면, 표면은 빛이 도달한 각도에 따라 다르게 조명이 되요.

만약 빛이 표면으로부터 수직으로 들어오면, 작은 표명에 집중되겠죠. 지금 보고 있는(시야) 각도에 도달하면, 같은 빛이 더 넓은 표면에 확산될 거에요 :

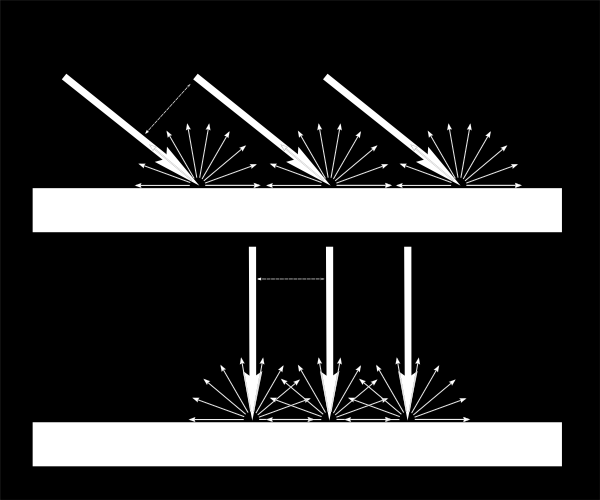
그러니까. 표면의 각 점은 수직보다는 응시각도일 때 더 어두워보이겠죠? 왜냐하면 상대적으로 더 적은 빛이 들어오니까요. (하지만 기억하세요, 응시각도일때 더 많은 빛이 조명될거니. 결국 최종적으로는 같을거에요. )

각 점이라는 말은 . 우리는 각각의 픽셀의 색상을 계산할 때 들어오는 빛과 표면 간의 각도가 중요하다는 것이죠. 이렇게 해볼 수 있을 것 같네요 :

// 빛과 법선사이의 각도에 대해 cosine을 구할게요. (실제로 cos함수를 쓰지는 않아요. 왜냐하면 연산량을 먹을 뿐더러, 두 벡터가 단위 벡터(길이가 1이라면)라는 가정하에서 내적은 두 벡터의 각도의 cos 과 같게 나오니까요. - 역주 )
// 법선 백터와 빛 백터 사이의 코사인 각도. 
// 0으로 clamp 됨. 
//  - 빛이 삼각형에 대해서 수직임. -> 1
//  - 빛이 삼각형에 대해서 수평임.  -> 0
float cosTheta = dot( n,l );

color = LightColor * cosTheta;

이 코드에서는, n은 표면의 법선이고, l은 표면으로 가는 빛의 단위 벡터에요. (표현이 글러먹은 것 같지만. 이게 좀… 직관적일거에요. 수학을 쉽게 만드려고 했어요.)

사인을 조심하세요.

우리의 cosTheta 공시에 뭐가 빠진 것 같아요. 빛이 삼각형 뒤에 있으면, n과 l이 뒤에 있다는 말이니까… n과 l의 내적은 음수가 되겠네요. 그러면 color = 음수숫자 가 되버리는데. 그건 그리 좋지 않을 것 같아요. 그러니까 cosTheat를 0으로 clamp 합시다. :

// 법선 백터와 빛 백터 사이의 코사인 각도. 
// 0으로 clamp 됨. 
//  - 빛과 법선이 수직이면 -> 1
//  - 빛과 법선이 수평이면 -> 0
//  - 빛이 삼각형 뒤에 있으면 ->0 
float cosTheta = clamp( dot( n,l ), 0,1 );

color = LightColor * cosTheta;

Material 색깔

물론, 출력 색상도 재질의 색상에 따라 다르겠죠. 이 이미지에서 흰색 빛은 녹색, 빨간색과 파란색 빛으로 만들어져요. 적색으로 뒤덮인 물체랑 충돌하면, 녹색과 청색 빛은 흡수디고 적색만 남겠죠?

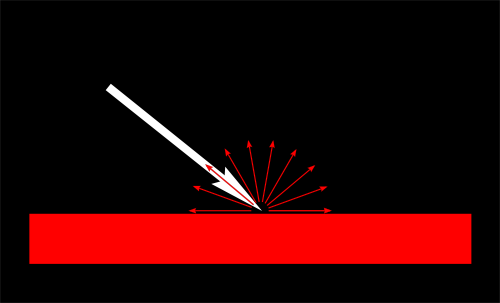
우리는 이걸 간단한 곱샘으로 표현할 수 있어요 : We can model this by a simple multiplication :

color = MaterialDiffuseColor * LightColor * cosTheta;

빛을 모델링하기.

자. 먼저 촛불이랑 비슷하게, 모든 방향으로 방출하는 빛을 가지고 있다고 가정해봐요.

그런 빛은 물질의 표면에 닿을 빛의 양이 광원까지의 거리에 따라 달라지겠죠? 멀리 떨어져 있을 수록 빚이 적죠. 실제로도, 빛의 양은 거리의 제곱으로 서서히 줄어들어요 :

color = MaterialDiffuseColor * LightColor * cosTheta / (distance*distance);

마지막으로, 우리는 빛의 세기를 조정할 매개변수가 필요하겠네요. 그걸 LightColor라고 정해요. (나중에 설명할 예정이에요. ) 그럼 이제, 우리는 빛의 색깔이랑 (예 : 흰색), 세기로 나타낼 수 있겠네요. (예 : 60 와트)

color = MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance);

다 넣어보기

자. 위에서 설명한 코드가 돌아가려면 매개 변수 몇개랑(아까 말한 색상과 힘이요.) 더 많은 코드가 필요해요.

MaterialDiffuseColor는 간단하게 텍스쳐에서 가져옵시다.

LightColor와 LightPower는 GLSL을 통해 셰이더로 보내면 될 것 같고요.

cosTheta는 n과 l에 의존하고 있죠. l은 어디서나 끌어오면 되는데. 카메라 공간에서 끌고 오는 게 제일 쉬워보이니까. 카메라 공간에서 끌어옵시다! :

 // fragment shader에서 계산된 법선, 카메라 공간 기준.
 vec3 n = normalize( Normal_cameraspace );
 // 빛의 방향. 
 vec3 l = normalize( LightDirection_cameraspace );

Normal_cameraspace와 LightDirection_cameraspace는 Vertex Shader에서 계산을 끝내고, fragment shader로 보내줄거에요 :

// 정점의 최종 좌표, 화면 상에선 : MVP * position
gl_Position =  MVP * vec4(vertexPosition_modelspace,1);

// 정점의 월드 좌표, 월드 공간에선 : M * position
Position_worldspace = (M * vec4(vertexPosition_modelspace,1)).xyz;

// 정점에서 카메라 공간을 향하는 벡터.
// 카메라 공간에선, 카메라는 원점에 있습니다. 
vec3 vertexPosition_cameraspace = ( V * M * vec4(vertexPosition_modelspace,1)).xyz;
EyeDirection_cameraspace = vec3(0,0,0) - vertexPosition_cameraspace;

// 카메라 공간에서 빛으로, 그리고 정점으로 가는 벡터. M은 단위 행렬 (숫자로 치면 1 - 역주) 이기에 생략했습니다.  
vec3 LightPosition_cameraspace = ( V * vec4(LightPosition_worldspace,1)).xyz;
LightDirection_cameraspace = LightPosition_cameraspace + EyeDirection_cameraspace;

// 카메라 공간에서 정점의 법선 벡터.
Normal_cameraspace = ( V * M * vec4(vertexNormal_modelspace,0)).xyz; // Only correct if ModelMatrix does not scale the model ! Use its inverse transpose if not.

이 코드는 Tutorial 3 : 메트릭스랑 비슷하게 보이지만. 거기서 배웠던 거랑 달라요. 아. 유의할 점이 하나 있어요. 지금 코드에는 각 벡터의 이름에 어느 공간인지 표시해주고 있죠? (예를 들면, Normal_cameraspace처럼요. - 역주) 이렇게 하면 이 벡터를 잘못 쓸 일이 없을거에요! 잘못 쓸 일이 뭐냐고요? 예를 들면 월드 공간에 있는 걸 카메라 공간이랑 곱하는 일을 피할 수 있어요. 피트랑 미터법이 다른 것처럼. 그런 원천적인 실수를 봉인할 수 있죠.

이렇게 길게 설명한 이유는 다들 아실거에요. 당연히 이걸 보는 여러분도 이렇게 하셔야 해요!

는 모델과 뷰 행렬을 말하는데요, MVP와 같은 방식으로 넘겨주시면 되요.

일할 시간!

자. 이제 Diffuse Lighting에 필요한 모든 코드가 준비 되었어요. 먼저 해보시고, 열심히 배워봐요! :)

결과

Diffuse만 사용하면, 이런 결과가 나올 거에요. (구린 텍스쳐에 다시 한 번 사과드려요) :

저번보다는 괜찮지만, 뭔가 많이 빠진 것 같네요. 특히. Clamp를 써서 그런가 모델링의 뒤는 완전히 검은색이에요.

주변광

주변광은 엄청나게 멋져요.

봐요. 실제 상황에서는 렘프의 빛이 벽에 부딪치고, 그게 반사되고, 반사되고, 반사되서 결국 모델링의 뒤에 빛이 조금이라도 갈거에요. 그런데 지금은 어떻죠? 그냥 검정색이죠.

그런데. 그걸 진짜로 다 계산하기에는 너무 시간이 많이 걸려요.

그래서, 일반적인 편법은 간단히 약간의 가짜 빛을 추가하는거죠. 그러니까. 3D 모델이 약간의 빛을 자체적으로 방출해서 완벽하게 검은 색으로 보이지 않게 하는거에요.

그럼. 이렇게 짤 수 있겠죠? :

vec3 MaterialAmbientColor = vec3(0.1,0.1,0.1) * MaterialDiffuseColor;

color =
 // 주변 광 : 간접광을 시뮬레이션 합니다. 
 MaterialAmbientColor +
 // 확산 광 : 오브젝트의 "색깔"입니다. 
 MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) ;

무슨 결과가 나오는 지 한번 봅시다!

결과

오. 좀 더 괜찮아 보이네요. 만약에 더 괜찮은 결과를 보고 싶으시면, (0.1, 0.1, 0.1)로 조정해도 될 것 같아요.

반사광

반사되는 빛의 대부분은, 표면에서 빛이 들어오는 방향으로 반사되요. 그게 반사광이죠.

이미지에서 볼 수 있듯. 일종의 로브(망토처럼 퍼져 보이죠? - 역주)를 형성해요. 하지만 극단적일 경우엔 확산 요소가 없을 지도 모르니. 로브는 아주, 아주, 아주 작을 지도 모르죠. (모든 빛은 단일 방향으로 반사되니까요.) 그러면 - 거울이 되는 거에요. 모든 빛을 정반사하니까요.

(거울을 만들려고 매개 변수를 조정할 수는 있겠는데. 지금 경우에는 반사할 수 있는게 광원 밖에 없어요. 그건 거울이 아니라, 가짜 거울이죠.)

// 눈 벡터 - 카메라 쪽.
vec3 E = normalize(EyeDirection_cameraspace);
// 삼각형이 빛을 반사하는 방향. 
vec3 R = reflect(-l,n);
// 눈 벡터와 반사 벡터 사이의 코사인 각도, 
// 0으로 clamp 됨. 
//  - 반사광을 들어다보고 있으면 -> 1
//  - 다른 곳을 보고 있으면 -> < 1
float cosAlpha = clamp( dot( E,R ), 0,1 );

color =
    // 주변광 : 간접 조명 시뮬레이션 
    MaterialAmbientColor +
    // 확산광 : 오브젝트의 "색깔" 
    MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) +
    // 반사광 : 반사 하이라이트, 거울 같이. 
    MaterialSpecularColor * LightColor * LightPower * pow(cosAlpha,5) / (distance*distance);

R은 빛의 반사 방향이에요. E는 눈(우리가”l”이라고 말한거 말이에요.)의 반대 방향이고요; 만약에 이 둘 사이에 각도가 작으면, 반사광을 똑바로 보고 있음을 말하는 거겠죠?

pow(cosAlpha,5)는 반사광의 로브의 넓이를 조정하는 데 쓸 수 있어요. 5보다 더 증가하면 - 얇은 로브를 얻을 수 있죠. (아마, 지금 반사하는 곳을 ‘로브’같다고 해서 로브라고 하는 것 같아요 - 역주 )

최종 결과

코와 눈쪽에 반사 하이라이트가 있는 거, 보이시죠?

이 쉐이딩 방법은 간단해서 수년 동안 사용되어 왔는데요. 하지만 여러가지 문제가 있어서, microfaect BRDF같은 물리 -기반-렌더링으로 대체되고 있어요. 그건 나중에 알아봐요.

다음 튜토리얼에선, VBO라는 것을 이용해서 성능을 어떻게 높일지 알아볼거에요! 그게 첫 중급 튜토리얼이 될거에요! 그러니까. 초급 튜토리얼은 끝났어요! 여기까지 따라와주신 여러분들. 축하드려요! 그럼 힘내서 중급 튜토리얼까지 가봅시다!