このチュートリアルではすこしOpenGLの領域を外れたことを説明します。しかしとても一般的な問題です。どうやって回転を表現するか？です。

チュートリアル3行列では特定の軸周りで点を回転させる行列を学びました。行列は頂点を変換するには良い方法ですが、行列を扱うのは難しいです。例えば、最終的な行列から回転軸を得るのはとてもトリッキーです。

回転を表す一般的な二つの方法を紹介します。オイラー角とクォータニオンです。最も重要なことは、なぜクォータニオンを使うべきかという理由を説明するところです。

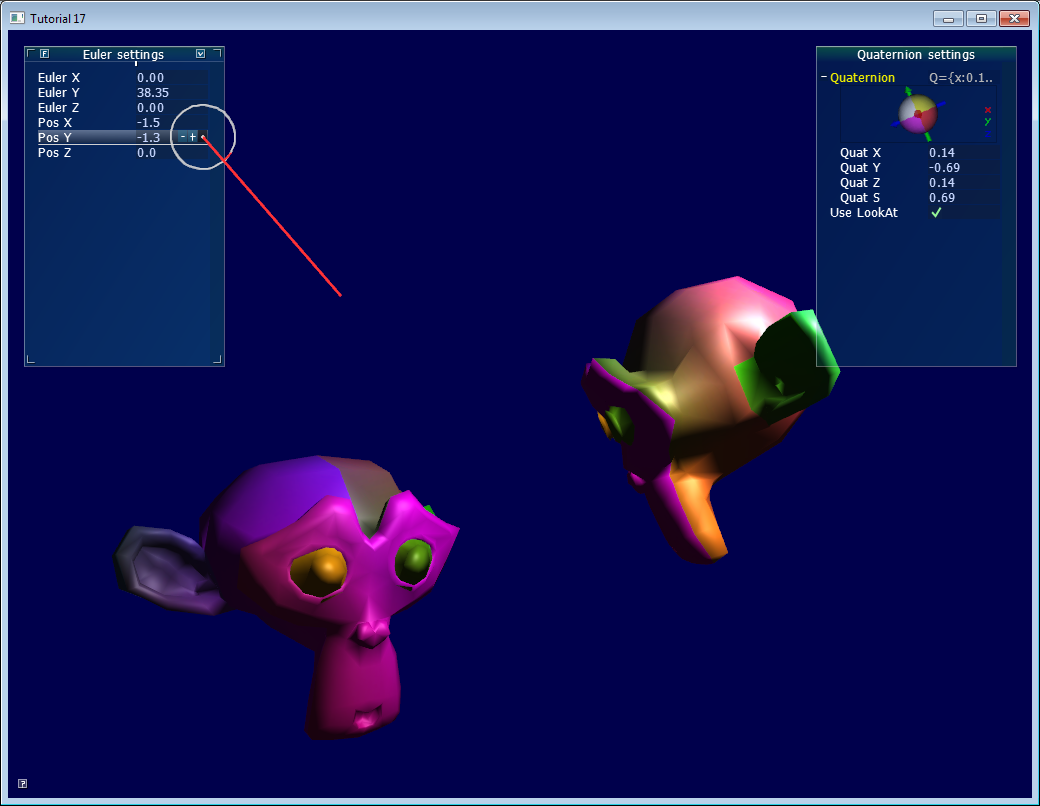
序文：回転と方向

回転に関する記事を読んでいる間、きっと語彙によって混乱が生じるでしょう。このチュートリアルでは次のようなものがあります。

  • 方向は状態です。”オブジェクトの方向は…”
  • 回転は操作です。”オブジェクトに回転を適用する。”

これはつまり 回転を適用 すれば 方向が変わる ということです。同じようなツールとして表現できるがゆえに混乱を招きます。それでは説明をしていきます。

オイラー角

オイラー角は回転を考える上で最も簡単な方法です。基本的にX、Y、Z軸周りでの3つの回転を格納するだけです。理解しやすいシンプルな概念です。それを格納するためにvec3を使います。

vec3 EulerAngles( RotationAroundXInRadians, RotationAroundYInRadians, RotationAroundZInRadians);

これらの3つの回転は連続的に実行されます。通常はY軸、Z軸、X軸の順番です。（ただし絶対ではありません。）異なる順番では異なる結果となります。

オイラー角のシンプルな使用方法の一つにキャラクターの方向をセットすることがあります。通常キャラクターはX軸やZ軸で回転せず、垂直軸だけで回転します。それゆえ、3つの異なる方向よりも、書くのも、理解するのも、軸を維持するのも簡単な方法となります。

他のオイラー角の使用方法にFPSカメラがあります。Y軸とX軸での角度のみを扱います。common/controls.cppを例として見てください。

しかし、より複雑になると、オイラー角でうまくやるには大変です。 例えば。

  • 二つの方向をスムーズに補間するのは大変です。単純にXとYとZの角度を補間してもひどい結果にしかなりません。
  • いくつかの回転を適用することは複雑で不正確なものです。最終的な回転行列を計算するには、この行列のオイラー角がどうなるかを考えなければなりません。
  • 良く知られた問題として、ジンバルロックがあります。これは時々回転をブロックしたり、モデルを上下逆さまにフリップするというような特性があります。
  • 異なる角度が同じ結果を表します。（例えば-180度と180度です。）
  • 上で挙げたように混乱を招きます。例えば正しい順番はYZXであるとか。しかしもし異なる順番のライブラリを使うと問題が生じます。
  • 複雑な操作もあります。例えばある軸でのN度の回転とかです。

クォータニオンはこれらの問題を解決する回転を表現するためのツールです。

クォータニオン

クォータニオンは4つの数字[x y z w]のセットで、次のように回転を表します。

// RotationAngleはラジアンで表します。
x = RotationAxis.x * sin(RotationAngle / 2)
y = RotationAxis.y * sin(RotationAngle / 2)
z = RotationAxis.z * sin(RotationAngle / 2)
w = cos(RotationAngle / 2)

RotationAxisは名前が示すとおり、回転させたい軸を表します。

RotationAngleはこの軸周りでの回転角度を示します。

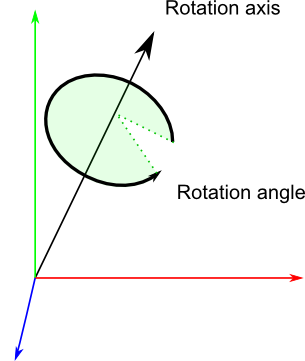
だからクォータニオンには 回転軸 と 回転角度 が必要となり、組み合わせることで回転を簡単にしています。

クォータニオンを読みこみ

フォーマットはオイラー角ほど直感的ではありませんが、解読は可能です。xyz要素はおおむね回転軸で、wは回転角のacosを2で割ったものを表します。例えばデバッガで次のような値を見たとしましょう。[ 0.7 0 0 0.7 ]、x=0.7はyとzより大きく、おおむねX軸周りで回転すると理解できるでしょう。そして2*acos(0.7) = 1.59ラジアン、つまりは90度の回転角で。

同様に[0 0 0 1] (w=1)はangle = 2acos(1) = 0ラジアンを意味し、これは *単位クォータニオン を意味し、何の回転も行いません。

基本的な操作

クォータニオンの背景にある数学を知ることにあまり意味はありません。表現はあまり直感的ではないので数学を実行してくれるようなユーティリティ関数にのみ頼ることになるでしょう。もし興味があれば Useful Tools & Linksにある数学本を読んでみてください。

どのようにC++でクォータニオンを作るか？

// #include <glm/gtc/quaternion.hpp>と<glm/gtx/quaternion.hpp>を忘れないで

// 単位クォータニオンを作る（何の回転もさせない）
quat MyQuaternion;

// 4要素の直接的な記述
// これを直接使うことはないでしょう。
MyQuaternion = quat(w,x,y,z); 

// オイラー角からラジアンのクォータニオンへの変換
vec3 EulerAngles(90, 45, 0);
MyQuaternion = quat(EulerAngles);

// 軸-角からの変換
// GLMでは角度は度で表すので、変換します。
MyQuaternion = gtx::quaternion::angleAxis(degrees(RotationAngle), RotationAxis);

GLSLでのクォータニオンの作りかた

できません。クォータニオンを回転行列に変換して、モデル行列で使います。頂点はいつもどおりMVP行列で回転されます。

多くの場合、GLSLでクォータニオンを使いたいでしょう。例えばGPU上でスケルタルアニメーションを実行したいときなどです。GLSLにはクォータニオンタイプはありません。しかし、vec4にひとまとめにできます。そしてシェーダ内であなた自身で数学を実行すれば良いのです。

クォータニオンの行列への変換方法

mat4 RotationMatrix = quaternion::toMat4(quaternion);

これでいつもどおりモデル行列を作れます。

mat4 RotationMatrix = quaternion::toMat4(quaternion);
...
mat4 ModelMatrix = TranslationMatrix * RotationMatrix * ScaleMatrix;
// MVP行列を作るためにモデル行列を使えます。

どちらを選ぶべきか？

オイラー角とクォータニオンの選択は難しいです。オイラー角は直感的で3Dエディタで書く場合には使うほうが良いでしょう。しかしクォータニオンはプログラマにとっては便利で、早いです。だから3Dエンジンコアではクォータニオンを使うべきです。

一般的には内部的にはクォータニオンを使い、ユーザインターフェースではオイラー角を使うべきです。

必要なもの（あるいは少なくとも簡単に）はすべて対処でき、必要とあればよりシンプルな変換であるオイラー角が使えます。（上で言ったようにカメラ、人型に適しています。）

他の資料

チートシート

二つのクォータニオンが似てるかの確認方法

内積をとればそれらのベクトルの角度を出してくれます。もし値が1ならば、同じ方向を向いています。

クォータニオンでもまったく同じです。

float matching = quaternion::dot(q1, q2);
if ( abs(matching-1.0) < 0.001 ){
    // q1とq2は同じ
}

q1とq2間の角度を知りたい場合は内積のacos()を取れば良いです。

頂点への回転の適用方法

次のようにできます。

rotated_point = orientation_quaternion *  point;

しかしモデル行列で計算したい場合は、代わりに行列に変換すべきです。

回転の中心は常に原点です。他の点で回転させたい場合には次のようにします。

rotated_point = origin + (orientation_quaternion * (point-origin));

二つのクォータニオンの補間方法

これはSLERPと呼ばれています。球面線形補間とい言います。GLMではこれをミックスすることで行えます。

glm::quat interpolatedquat = quaternion::mix(quat1, quat2, 0.5f); // or whatever factor

二つの回転の計算方法

単純に二つのクォータニオンを掛け合わせるだけです。行列と同じで順番は同じです。つまり逆順です。

quat combined_rotation = second_rotation * first_rotation;

二つのベクトル間の回転の見つけ方

(言い換えれば、v2にマッチするようにv1を回転させるようなクォータニオン）

基本的な考え方は直接的です。

  • ベクトル同士の角度の見つけ方：内積でコサインが得られます
  • 回転角の見つけ方：二つのベクトルの外積

次のアルゴリズムがこれを行います。しかし特別なケースには対処が必要です。

quat RotationBetweenVectors(vec3 start, vec3 dest){
	start = normalize(start);
	dest = normalize(dest);

	float cosTheta = dot(start, dest);
	vec3 rotationAxis;

	if (cosTheta < -1 + 0.001f){
		// ベクトルが反対方向を向いている特殊なケース：
		// 単位回転軸はないので、垂直なものを見つけます。
		rotationAxis = cross(vec3(0.0f, 0.0f, 1.0f), start);
		if (gtx::norm::length2(rotationAxis) < 0.01 ) // 残念、平行なのでもう一度！
			rotationAxis = cross(vec3(1.0f, 0.0f, 0.0f), start);

		rotationAxis = normalize(rotationAxis);
		return gtx::quaternion::angleAxis(glm::radians(180.0f), rotationAxis);
	}

	rotationAxis = cross(start, dest);

	float s = sqrt( (1+cosTheta)*2 );
	float invs = 1 / s;

	return quat(
		s * 0.5f, 
		rotationAxis.x * invs,
		rotationAxis.y * invs,
		rotationAxis.z * invs
	);

}

この関数はcommon/quaternion_utils.cppにあります。

gluLookAtと同じように、オブジェクトをある点の方向へ向けさせたい。

RotationBetweenVectorsを使いましょう！

// オブジェクトの前方（通常は+Z方向ですが、場合によります）と目的の方向との回転を見つけます。
quat rot1 = RotationBetweenVectors(vec3(0.0f, 0.0f, 1.0f), direction);

ここでオブジェクトをまっすぐ向かせたい場合を考えます。

// 方向と垂直するように、目的の上方向を再計算します。
// もし本当に目的の上方向に向かせたいなら、このパートはスキップできます。
vec3 right = cross(direction, desiredUp);
desiredUp = cross(right, direction);

// 最初の回転のため、上はたぶん失敗します。
//オブジェクトの上と目的の上との間の角度を見つけます。
vec3 newUp = rot1 * vec3(0.0f, 1.0f, 0.0f);
quat rot2 = RotationBetweenVectors(newUp, desiredUp);

これらをあわせます。

quat targetOrientation = rot2 * rot1; // 逆順になります。

“方向”は方向であって目標とする点ではありません。しかし次のように位置は計算できます。目標点-現在点。

一度目的の方向を得たなら、startOrientationとtargetOrientationの間の補間が欲しいと思います。

（この関数はcommon/quaternion_utils.cppにあります。）

特定の回転スピードに制限したLookAtの使い方

基本的な考え方はSLERP( = use glm::mix )と同じです。しかし回転角が目的の値より大きくならないように補間します。

float mixFactor = maxAllowedAngle / angleBetweenQuaternions;
quat result = glm::gtc::quaternion::mix(q1, q2, mixFactor);

以下に特殊なケースにも対応した完璧な実装を示します。最適化のためmix()を直接は使っていません。

quat RotateTowards(quat q1, quat q2, float maxAngle){

	if( maxAngle < 0.001f ){
		// No rotation allowed. Prevent dividing by 0 later.
		return q1;
	}

	float cosTheta = dot(q1, q2);

	// q1とq2は既に同じです。
	// q2を返します。
	if(cosTheta > 0.9999f){
		return q2;
	}

	// 球の周りの長いパスを取るのを防ぎます。
	if (cosTheta < 0){
	    q1 = q1*-1.0f;
	    cosTheta *= -1.0f;
	}

	float angle = acos(cosTheta);

	// もし5度ずつ回転させてるときに2度しかない場合は到着させます。
	if (angle < maxAngle){
		return q2;
	}

	float fT = maxAngle / angle;
	angle = maxAngle;

	quat res = (sin((1.0f - fT) * angle) * q1 + sin(fT * angle) * q2) / sin(angle);
	res = normalize(res);
	return res;

}

これは次のように使います。

CurrentOrientation = RotateTowards(CurrentOrientation, TargetOrientation, 3.14f * deltaTime );

この関数はcommon/quaternion_utils.cppにあります。

他の方法は…

もしこれで解決しないなら、メールを送ってください、それをリストに追加します。