チュートリアル13:法線マッピング
ようこそチュートリアル13へ!ここでは法線マッピングについて説明します。
チュートリアル8で 、三角形の法線を使ってちゃんとしたシェーディングをする方法を学びました。これまでは、各頂点に対して一つの法線だけを扱ってきました。各三角形内では、テクスチャからサンプルした色はスムーズに変化していました。法線マッピングの基本的な考え方は、これと同様な方法で法線を与えることです。
法線テクスチャ
”法線テクスチャ”は次のようなものです。

各RGBテクセルはXYZベクターに符号化されます。各色要素は0と1の間にあり、各ベクター要素は-1から1の間にあります。だからこのシンプルなマッピングはテクセルから法線へと変わっていきます。
normal = (2*color)-1 // 各要素
テクスチャは一般的に青色です。なぜなら法線は”面の外側”に向かっているからです。いつもどおり、Xはテクスチャの右方向を、Yは上方向を表します。だから右手の法則により、法線はテクスチャの面の外側へ向かってることを意味します。
このテクスチャはちょうど拡散光と同じようにマッピングされます。ここで、各三角形の空間(接空間、あるいはイメージ空間とよばれます)で表されている法線を、どのようにしてモデル空間へ変換するかが問題となります。
接空間と従接空間
空間を定義するためには3つのベクトルを必要とすることは分かると思います。(ここでは接空間を指します。)既に”上”は向かうベクトルを分かっているとします。これこそが法線で、Blenderや三角形から単純な外積によって計算されているとします。これは法線マップの全体的な色のように青色で表現されます。

次に接線Tが必要となります。つまり面に垂直なベクトルです。しかしそのようなベクトルはたくさんあります。

どれを選ぶべきでしょうか?理論的にはどれでもよいのですが、醜いエッジが出るのを避けるためには、周囲と調和しているものを選ぶ必要があります。一般的な方法は接線をテクスチャ座標と同じ方向に向かせることです。
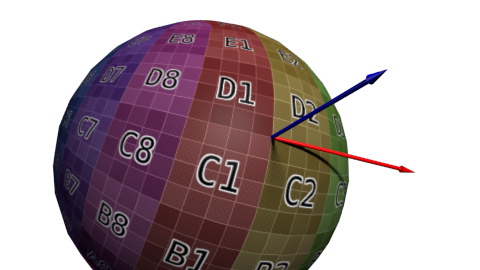
基底を定義するには3つのベクトルが必要になるので、従接線Bを計算しなければなりません。(これはどれか他の接線ですが、すべてのベクトルが垂直ならば、計算が楽になります。)
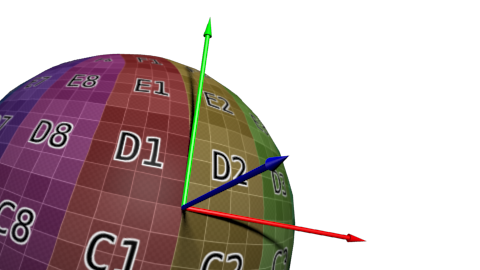
ここにアルゴリズムを示します。deltaPos1とdeltaPos2を三角形の2線を、deltaUV1とdeltaUV2がUV座標での差を表すとすると、次のような等式で問題を表現できます。
deltaPos1 = deltaUV1.x * T + deltaUV1.y * B
deltaPos2 = deltaUV2.x * T + deltaUV2.y * B
ただこれをTとBに対して解くだけで、ベクトルが得られます。(下のコードを見てください。)
いまTとBとNベクトルが得られたとすると、この行列が接空間からモデル空間への変換を可能にしてくれます。
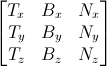
ただこれをTとBに対して解くだけで、ベクトルが得られます。(下のコードを見てください。)いまTとBとNベクトルが得られたとすると、この行列が接空間からモデル空間への変換を可能にしてくれます。このTBN行列により、(テクスチャから得られた)法線をモデル空間へ変換できます。しかし通常は別の方法が使われます。すべてをモデル空間から接空間へ変換し、法線をそのままの状態にしておきます。すべての計算を接空間で行っても、なにも変わりません。
逆変換は単純に逆行列を計算することで得られます。すべてのベクトルが他のベクトルと直交する直交行列なので、安い計算コストで得られる転置行列が逆行列となります。
invTBN = transpose(TBN)
, i.e. :
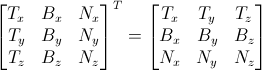
VBOの準備
接線と従接線の計算
法線に対応する接線と従接線が必要となるので、すべてのメッシュに対して計算しなければなりません。これは個別の関数で実装しています。
void computeTangentBasis(
// 入力
std::vector<glm::vec3> & vertices,
std::vector<glm::vec2> & uvs,
std::vector<glm::vec3> & normals,
// 出力
std::vector<glm::vec3> & tangents,
std::vector<glm::vec3> & bitangents
){
各三角形に対して、エッジ(deltaPos)とdeltaUVを計算します。
for ( int i=0; i<vertices.size(); i+=3){
// Shortcuts for vertices
glm::vec3 & v0 = vertices[i+0];
glm::vec3 & v1 = vertices[i+1];
glm::vec3 & v2 = vertices[i+2];
// Shortcuts for UVs
glm::vec2 & uv0 = uvs[i+0];
glm::vec2 & uv1 = uvs[i+1];
glm::vec2 & uv2 = uvs[i+2];
// Edges of the triangle : postion delta
glm::vec3 deltaPos1 = v1-v0;
glm::vec3 deltaPos2 = v2-v0;
// UV delta
glm::vec2 deltaUV1 = uv1-uv0;
glm::vec2 deltaUV2 = uv2-uv0;
以下の式で接線と従接線を計算します。
float r = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV1.y * deltaUV2.x);
glm::vec3 tangent = (deltaPos1 * deltaUV2.y - deltaPos2 * deltaUV1.y)*r;
glm::vec3 bitangent = (deltaPos2 * deltaUV1.x - deltaPos1 * deltaUV2.x)*r;
最後に、tangentsとbitangentsとbuffers をセットします。注意することはこれらのバッファはまだインデックスされた居ない点です。だから各頂点はそれ自身のコピーを持っています。
// 三角形の3頂点すべてに同じ接線をセットします。
// これらは後でvboindexer.cppにてマージされます。
tangents.push_back(tangent);
tangents.push_back(tangent);
tangents.push_back(tangent);
// 従接線に対しても同じ処理をします。
bitangents.push_back(bitangent);
bitangents.push_back(bitangent);
bitangents.push_back(bitangent);
}
インデックス
このVBOをインデックスする方法はこれまでと似ていますが、少し違う部分があります。
似たような頂点(同じ位置、同じ法線、同じテクスチャ座標)を見つけたとき、それ自身の接線や従接線を使ってほしくありません。代わりにに平均化したそれらを使います。だから古いコードを少し修正しましょう。
// out_XXXXにある似た頂点を見つけましょう。
unsigned int index;
bool found = getSimilarVertexIndex(in_vertices[i], in_uvs[i], in_normals[i], out_vertices, out_uvs, out_normals, index);
if ( found ){ // 似たような頂点が既にVBOにあります、代わりにそれを使いましょう!
out_indices.push_back( index );
// 接線と従接線を平均化する
out_tangents[index] += in_tangents[i];
out_bitangents[index] += in_bitangents[i];
}else{ //もしなければ出力データに追加します。
// いつもどおり
[...]
}
ここでは正規化は行いません。小さな接線と従接線を持つ小さな三角形は、大きな三角形に比べて最終的なベクトルに小さな影響を与えるため、このようにします。
シェーダ
追加のバッファとユニフォーム
接線と従接線用の新たに二つのバッファが必要となります。
GLuint tangentbuffer;
glGenBuffers(1, &tangentbuffer);
glBindBuffer(GL_ARRAY_BUFFER, tangentbuffer);
glBufferData(GL_ARRAY_BUFFER, indexed_tangents.size() * sizeof(glm::vec3), &indexed_tangents[0], GL_STATIC_DRAW);
GLuint bitangentbuffer;
glGenBuffers(1, &bitangentbuffer);
glBindBuffer(GL_ARRAY_BUFFER, bitangentbuffer);
glBufferData(GL_ARRAY_BUFFER, indexed_bitangents.size() * sizeof(glm::vec3), &indexed_bitangents[0], GL_STATIC_DRAW);
新たな法線テクスチャ用の新たなユニフォームも必要となります。
[...]
GLuint NormalTexture = loadTGA_glfw("normal.tga");
[...]
GLuint NormalTextureID = glGetUniformLocation(programID, "NormalTextureSampler");
3x3のモデルビュー行列も作ります。実際は必要ではありませんが、後で述べるようにより簡単になります。方向だけを掛けるため、行列の左上の3x3部分だけが必要です。そのため平行移動部分は使いません。
GLuint ModelView3x3MatrixID = glGetUniformLocation(programID, "MV3x3");
最終的なコードは次のようになります。
// スクリーンをクリアする
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
// シェーダを使う
glUseProgram(programID);
// キーボードとマウスの入力からMVP行列を計算する
computeMatricesFromInputs();
glm::mat4 ProjectionMatrix = getProjectionMatrix();
glm::mat4 ViewMatrix = getViewMatrix();
glm::mat4 ModelMatrix = glm::mat4(1.0);
glm::mat4 ModelViewMatrix = ViewMatrix * ModelMatrix;
glm::mat3 ModelView3x3Matrix = glm::mat3(ModelViewMatrix); // Take the upper-left part of ModelViewMatrix
glm::mat4 MVP = ProjectionMatrix * ViewMatrix * ModelMatrix;
// MVPユニフォームで、今使っているシェーダに変換を送る。
glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &MVP[0][0]);
glUniformMatrix4fv(ModelMatrixID, 1, GL_FALSE, &ModelMatrix[0][0]);
glUniformMatrix4fv(ViewMatrixID, 1, GL_FALSE, &ViewMatrix[0][0]);
glUniformMatrix4fv(ViewMatrixID, 1, GL_FALSE, &ViewMatrix[0][0]);
glUniformMatrix3fv(ModelView3x3MatrixID, 1, GL_FALSE, &ModelView3x3Matrix[0][0]);
glm::vec3 lightPos = glm::vec3(0,0,4);
glUniform3f(LightID, lightPos.x, lightPos.y, lightPos.z);
// 拡散テクスチャをテクスチャユニット0としてバインドする
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, DiffuseTexture);
// "DiffuseTextureSampler"をテクスチャユニット0としてセットする
glUniform1i(DiffuseTextureID, 0);
// 法線テクスチャをテクスチャユニット1としてバインドする
glActiveTexture(GL_TEXTURE1);
glBindTexture(GL_TEXTURE_2D, NormalTexture);
// "Normal TextureSampler"をテクスチャユニット0としてセットする。
glUniform1i(NormalTextureID, 1);
// 最初の属性バッファ:頂点
glEnableVertexAttribArray(0);
glBindBuffer(GL_ARRAY_BUFFER, vertexbuffer);
glVertexAttribPointer(
0, // 属性
3, //サイズ
GL_FLOAT, // タイプ
GL_FALSE, // 正規化?
0, // ストライド
(void*)0 // 配列バッファオフセット
);
// 2番目の属性バッファ:UV
glEnableVertexAttribArray(1);
glBindBuffer(GL_ARRAY_BUFFER, uvbuffer);
glVertexAttribPointer(
1, // 属性
2, // サイズ
GL_FLOAT, // タイプ
GL_FALSE, // 正規化?
0, // ストライド
(void*)0 // 配列バッファオフセット
);
// 3番目の属性バッファ:法線
glEnableVertexAttribArray(2);
glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
glVertexAttribPointer(
2, // 属性
3, // サイズ
GL_FLOAT, // タイプ
GL_FALSE, // 正規化?
0, // ストライド
(void*)0 // 配列バッファオフセット
);
// 4番目の属性バッファ:接線
glEnableVertexAttribArray(3);
glBindBuffer(GL_ARRAY_BUFFER, tangentbuffer);
glVertexAttribPointer(
3, // 属性
3, // サイズ
GL_FLOAT, // タイプ
GL_FALSE, // 正規化?
0, // ストライド
(void*)0 // 配列バッファオフセット
);
// 5番目の属性バッファ:従接線
glEnableVertexAttribArray(4);
glBindBuffer(GL_ARRAY_BUFFER, bitangentbuffer);
glVertexAttribPointer(
4, // 属性
3, // サイズ
GL_FLOAT, // タイプ
GL_FALSE, // 正規化?
0, // ストライド
(void*)0 // 配列バッファオフセット
);
// インデックスバッファ
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, elementbuffer);
// 三角形を描く!
glDrawElements(
GL_TRIANGLES, // モード
indices.size(), // カウント
GL_UNSIGNED_INT, //タイプ
(void*)0 // 要素配列バッファオフセット
);
glDisableVertexAttribArray(0);
glDisableVertexAttribArray(1);
glDisableVertexAttribArray(2);
glDisableVertexAttribArray(3);
glDisableVertexAttribArray(4);
// バッファを入れ替える
glfwSwapBuffers();
頂点シェーダ
以前言ったように、カメラ空間ですべてを行います。なぜならこの空間ではフラグメントの位置をより簡単に取得できるからです。これがT、B、Nベクターにモデルビュー行列を掛けた理由です。
vertexNormal_cameraspace = MV3x3 * normalize(vertexNormal_modelspace);
vertexTangent_cameraspace = MV3x3 * normalize(vertexTangent_modelspace);
vertexBitangent_cameraspace = MV3x3 * normalize(vertexBitangent_modelspace);
これらの3つのベクトルはTBN行列として定義され、次のように構築します。
mat3 TBN = transpose(mat3(
vertexTangent_cameraspace,
vertexBitangent_cameraspace,
vertexNormal_cameraspace
)); // この行列を作って変換する代わりに内積でもできます。参考文献を読んでみてください。
この行列でカメラ空間から接空間へ移ります。代わりにXXX_modelspaceという同じ行列でもモデル空間から接空間への変換が行われます。これを接空間でのライトと目の方向を計算するために使います。
LightDirection_tangentspace = TBN * LightDirection_cameraspace;
EyeDirection_tangentspace = TBN * EyeDirection_cameraspace;
フラグメントシェーダ
接空間での法線はテクスチャから直接得られます。
// 接空間でのローカル法線
vec3 TextureNormal_tangentspace = normalize(texture( NormalTextureSampler, UV ).rgb*2.0 - 1.0);
これで必要なものはすべてそろいました。拡散光は clamp( dot( n,l ), 0,1 ) を使います。 nとlは接空間で表されています。(内積や外積をとる場合、2ベクトルがどの空間にあるかは問題ではありませんが、同じ空間にある必要があります。)鏡面光では clamp( dot( E,R ), 0,1 ) を使います。同様にEとRは接空間で表現されています。
結果
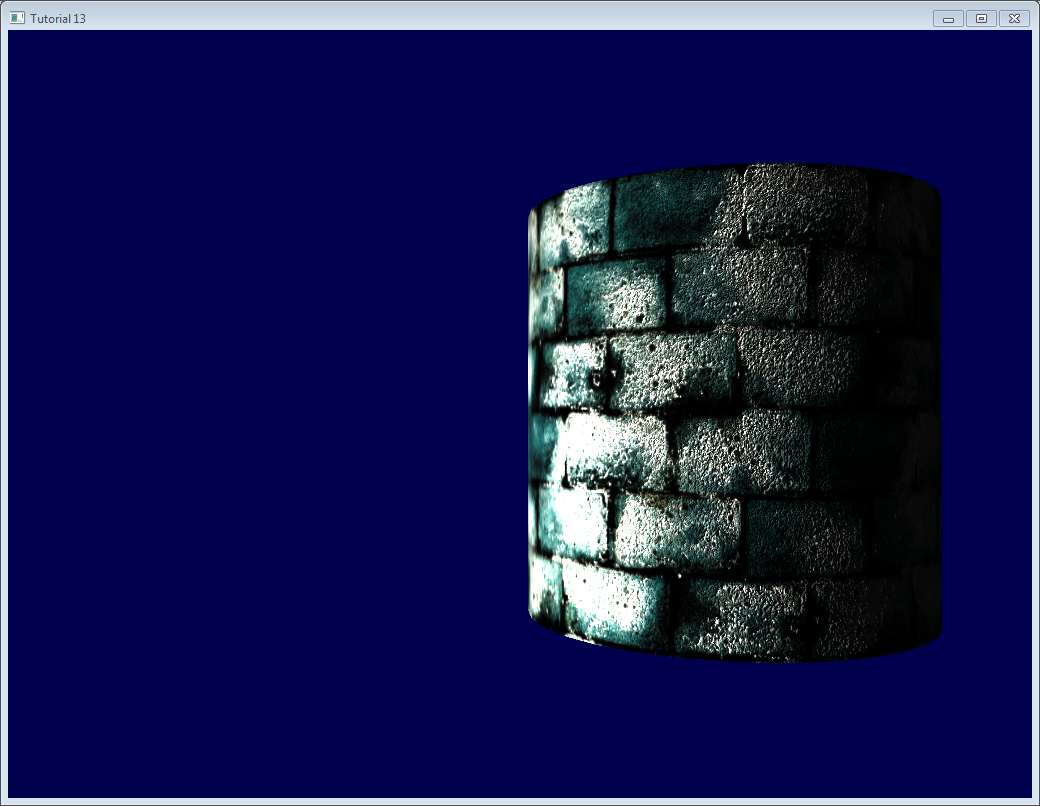
結果を示しておきます。次のことに気づくでしょう
- 様々な種類の法線を使っているので、レンガがでこぼこに見える。
- 法線テクスチャは一様に青いので、セメントは平面的に見える。

さらに先へ
##直交化
頂点シェーダでは逆行列の変わりに転置行列を使いました。しかしこれは行列が表す空間が直交してることが前提です。幸運なことに、まだそういう状態でないときでも簡単に修正できます。TangentBasis()を計算する最後のほうで法線に直交するように接線を作る必要があります。
t = glm::normalize(t - n * glm::dot(n, t));
上の式は理解しづらいかもしれません。以下の図が参考になります。
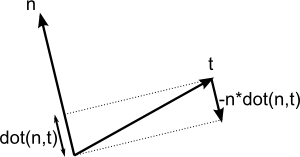
nとtはほぼ垂直です。だからtを-n倍したdot(n,t)方向へ押せば良いのです。
ここにこれを説明するアプレットがここにあります。(2ベクトルの場合)
利き手
通常それについて悩む必要はありませんが、対象のモデルを使うような特殊なケースでは、UVは間違った方向を向き、Tは間違った方向になります。
逆にすべきかどうかを判断するのはとても簡単です。TBNは右手座標系でなければなりません。つまりcross(n,t)はbと同じ方向を向きます。
数学的には、ベクトルAとベクトルBが同じ方向を向いているというのは、dot(A,B)>0と表せます。だからdot( cross(n,t) , b ) > 0かどうかをチェックする必要があります。もし負ならば逆にします。
If it’s false, just invert t :
if (glm::dot(glm::cross(n, t), b) < 0.0f){
t = t * -1.0f;
}
TangentBasis()を計算し終わったときに、各頂点で同様の処理をします。
鏡面テクスチャ
よりおもしろくするために、鏡面テクスチャをコードに追加しました。それは次のようなものです。

そして単純な灰色“vec3(0.3,0.3,0.3)”の鏡面光の代わりに使います。
これでセメントは常に黒くなりました。なぜならテクスチャが鏡面光はないものとしているからです。
immediateモードによるデバッグ
このウェブサイトの本当の目的は、あなたがimmediateモードを使わないようにすることです。immediateモードは遅いなど様々な面で問題を抱えています。
しかし、デバッグのためにはとても便利です。
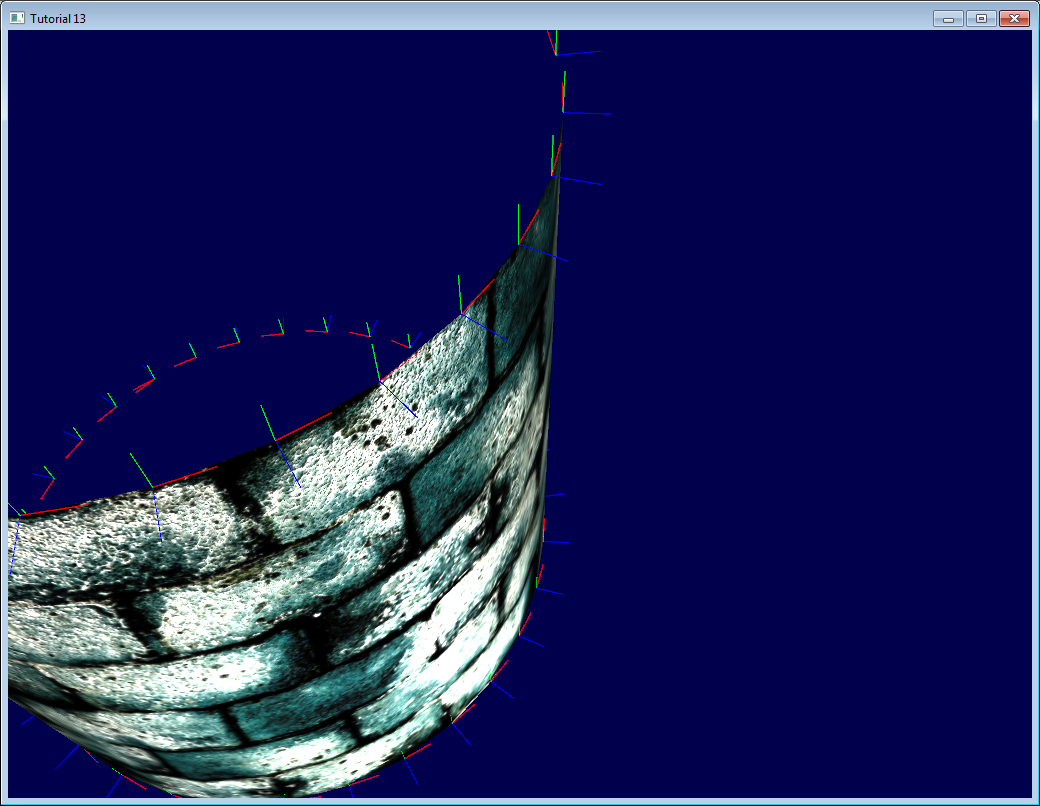
ここにimmediateモードで接空間を線で可視化しました。
このためには、3.3 core profileを捨てる必要があります。
glfwOpenWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_COMPAT_PROFILE);
そして行列を古いOpenGLのパイプラインに渡します。(他のシェーダでもできますが、これがよりシンプルな例です。)
glMatrixMode(GL_PROJECTION);
glLoadMatrixf((const GLfloat*)&ProjectionMatrix[0]);
glMatrixMode(GL_MODELVIEW);
glm::mat4 MV = ViewMatrix * ModelMatrix;
glLoadMatrixf((const GLfloat*)&MV[0]);
シェーダを無効化します。
glUseProgram(0);
そして線を描画します。(この場合、法線を正規化して0.1を掛けて、正しい頂点に適用します。)
glColor3f(0,0,1);
glBegin(GL_LINES);
for (int i=0; i<indices.size(); i++){
glm::vec3 p = indexed_vertices[indices[i]];
glVertex3fv(&p.x);
glm::vec3 o = glm::normalize(indexed_normals[indices[i]]);
p+=o*0.1f;
glVertex3fv(&p.x);
}
glEnd();
注意:immediateモードはデバッグ以外では使わないでください。そしてcore profileを後で有効化するのを忘れないでください。
色によるデバッグ
デバッグするとき、ベクトルの値を可視化できると便利です。最も簡単な方法は、フラグメントシェーダで実際の色の代わりに使うことです。
color.xyz = LightDirection_tangentspace;
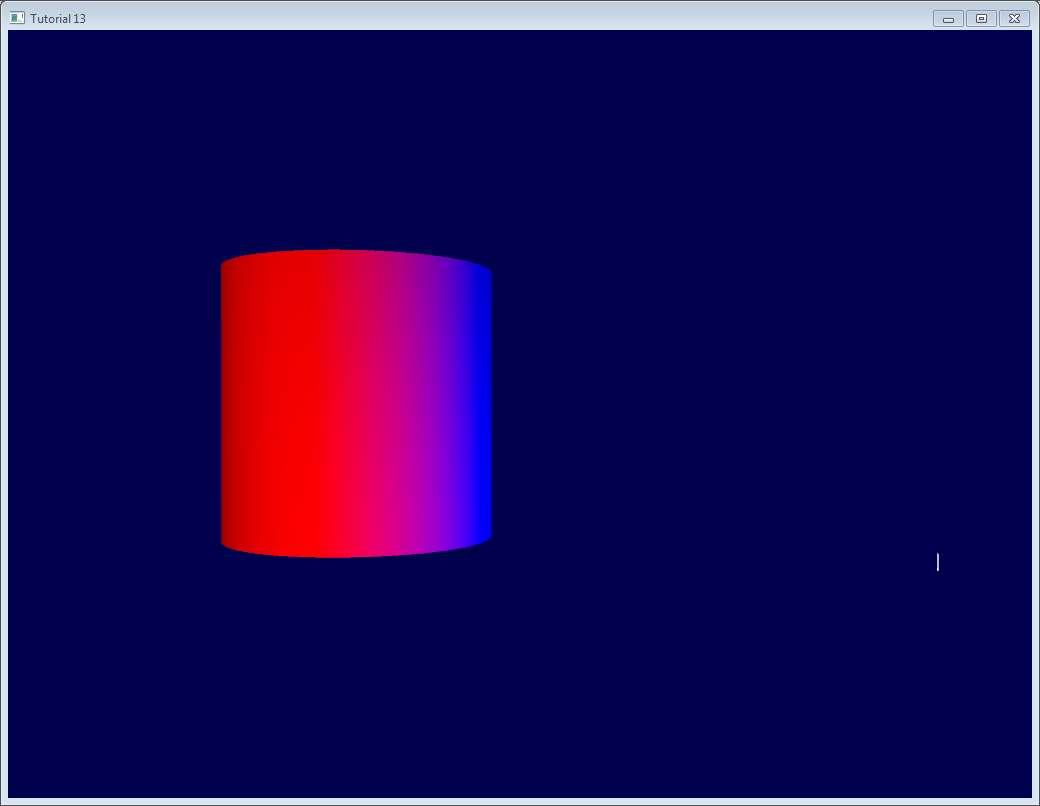
これは次のことを意味します。
- 円柱の右側では、(小さな白い線で表現されている)光は(接空間で)上を向いていることを意味します。言い換えれば、光は三角形の法線の方向を向いています。
- 円柱の中央では、光は接線(+X)方向を向いています。
チップス:
- 何を可視化したいかにもよりますが、それを正規化したいでしょう。
- 見えているものが何か理解できないときは、すべての要素を分解して可視化しましょう。例えば緑と青を0にするとか。
- アルファには手を出さないようにしましょう。とっても複雑です。:)
- 負の値を可視化したい場合は、通常のテクスチャを使うときと同じようなトリックが使えます。つまりかわりに(v+1.0)/2.0を使います。すると黒は-1をフルカラーは+1を意味します。とはいっても、見ているものを理解するのは難しいですが。
変数名でデバッグ
既に以前言ったように、ベクトルがどの空間にあるかはとても重要です。カメラ空間にあるベクトルとモデル空間にあるベクトルとの内積は取ってはいけません。
変数名にベクトルがある空間名を(“…_modelspace”のように)追加する と数学的なバグを修正するのがとても簡単になります。
法線マップの作り方
James O’Hareによる作りかた。クリックで拡大してください。

演習
- 加える前にindexVBO_TBNにあるベクトルを正規化して可視化してみましょう。
- 他のベクトル(例えば、EyeDirection_tangentspace)もカラーモードで可視化してみましょう。そしてそれが何を意味するか理解してみましょう。
ツールとリンク
- Crazybump , 法線マップを作るのに適しています。有料です。
- Nvidia’s photoshop plugin. 無料です。でもフォトショップが必要です。
- Make your own normal maps out of several photos
- Make your own normal maps out of one photo
- より詳しいことは matrix transposeにあります。