• 法線
  • 三角形の法線
  • 頂点法線
  • OpenGLでの頂点法線の使用方法
• 拡散光
  • 表面法線の重要性
  • 符号に関する注意
  • 物体の色
  • 光のモデル化
  • すべてを合わせる
  • 実行
  • 結果
• 環境光
  • 結果
• 鏡面光
  • Final result

チュートリアル8では、基本的なシェーディングについて学びます。ここでは次のことを学びます。 In this 8th tutorial, we will learn how to do some basic shading. This includes :

• 光源に近ければより光らせます。
• 光の反射によるハイライト(鏡面光)
• 光が直接向かっていなければ暗く見えます。(拡散光)
• その他（環境光）

次のことは学びません。

• 影、複数のチュートリアルで扱います。
• 鏡のような反射(水も含みます。)
• 表面に広がったような洗練された光るもの(ワックスのようなものです。)
• 異方性の物質(磨かれた物体のようなものです。)
• より現実に近いものを表現しようとする物理ベースのシェーディング
• アンビエントオクルージョン(洞窟のなかのようなものです。)
• 色のブレンド(赤いカーペットは白い天井をほんのすこし赤くします。)
• 透明
• 大域照明(上で挙げたものをまとめた名前です。)

要するに基礎だけです。

法線

これまでのチュートリアルでは、法線の本当の意味を理解せずに使ってきました。

三角形の法線

平面の法線とはその平面に垂直な長さが1のベクトルです。

三角形の法線とはこの三角形に垂直で長さが1のベクトルです。法線は三角形の辺の2つの外積を取ることで簡単に計算できます。(aとbの外積はその二つに垂直なベクトルを作ります。覚えていますか？)そして正規化します。つまりそのベクトルの長さを1にします。擬似コードは次のとおりです。

triangle ( v1, v2, v3 )
edge1 = v2-v1
edge2 = v3-v1
triangle.normal = cross(edge1, edge2).normalize()

法線(normal)と正規化(normalize())を混同しないでください。normalize()は(法線とは限らない)ベクトルの長さでそのベクトル自身を割ることで長さを1にします。法線(normal)とは垂直線のベクトルを表す名前です。

頂点法線

三角形の法線の拡張で、ある頂点の周辺の三角形の法線の組み合わせを頂点の法線と呼びます。頂点シェーダでは三角形ではなく頂点を扱うので、これはとても便利です。だから頂点ごとに情報があるほうが良いのです。なにより、OpenGLでは三角形上の情報を持てません。擬似コードは次のとおりです。

vertex v1, v2, v3, ....
triangle tr1, tr2, tr3 // all share vertex v1
v1.normal = normalize( tr1.normal + tr2.normal + tr3.normal )

OpenGLでの頂点法線の使用方法

OpenGLで法線を使うのはとても簡単です。法線は頂点の属性です。だから位置や色、UV座標と同じようにいつもどおりやっていきます。チュートリアル7で作ったloadOBJローダはOBJファイルから既に法線情報を読み込んでいます。

GLuint normalbuffer;
 glGenBuffers(1, &normalbuffer);
 glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
 glBufferData(GL_ARRAY_BUFFER, normals.size() * sizeof(glm::vec3), &normals[0], GL_STATIC_DRAW);

and

 // 3つ目の属性：法線
 glEnableVertexAttribArray(2);
 glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
 glVertexAttribPointer(
     2,                                // 属性
     3,                                // サイズ
     GL_FLOAT,                         // タイプ
     GL_FALSE,                         // 正規化？
     0,                                // ストライド
     (void*)0                          // 配列バッファオフセット
 );

はじめるにはこれで充分です。

拡散光

表面法線の重要性

光が物に当たったとき、その一部は全方向に反射されます。これが拡散光です。(他の部分がどのようになるかは後で見ていきます。)

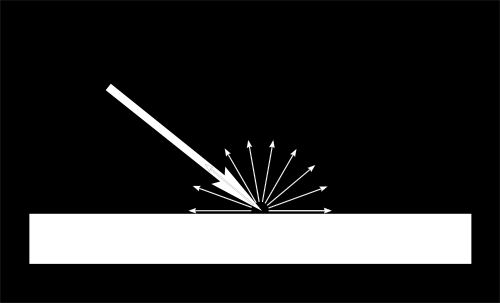
特定の光の束が表面に到着したとき、光が到達した角度に応じて違うように照らされます。

もし光が表面に垂直ならば、狭い表面上に集中します。もし光が熟視角で到達したならば、同じ量の光がより広い表面に広がっていきます。

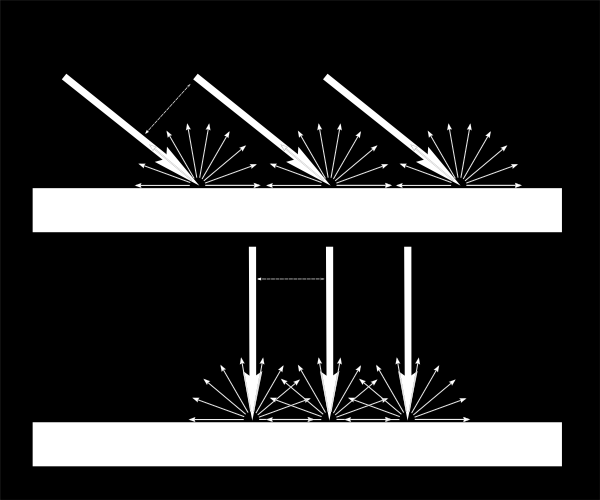
これは、熟視角で到達し光の場合、表面の各点はより暗く見えることを意味します。(ただし、より広い範囲が照らされます。つまり光の総量は変わりません。)

これは、ピクセルの色を計算するときに、光の入ってきた角度と表面の法線との角度が重要になることを意味します。次のことを得ます。

// 法線と光の方向の角度のコサイン
// 0以上に固定します。
//  - 光が三角形に水平の場合 -> 1
//  - 光が三角形に垂直の場合 -> 0
float cosTheta = dot( n,l );

color = LightColor * cosTheta;

ここでnは表面の法線で、lは表面から光に向かう方向の単位ベクトルを表します。(反対の方向ではありません。直感的ではありませんが、計算を簡単にします。)

符号に関する注意

上のcosThetaの式では何か忘れています。もし光が三角形の後ろにあると、nとlは反対になります。だからnとlは負になります。これは”色＝負の数”を意味しますがこれでは意味が分かりません。だからcosThetaの下限を0に固定します。

// 法線と光の方向の角度のコサイン
// clamped above 0
//  - 光が三角形に水平の場合 -> 1
//  - 光が三角形に垂直の場合 -> 0
//  - 光が三角形の裏側の場合 -> 0
float cosTheta = clamp( dot( n,l ), 0,1 );

color = LightColor * cosTheta;

物体の色

もちろん、アウトプットカラーは物体の色にも影響されます。この画像では白い光は緑・赤・青の光から構成されています。光が赤い物体にあたったとき、緑と青の光は吸収され、赤い光だけが残ります。

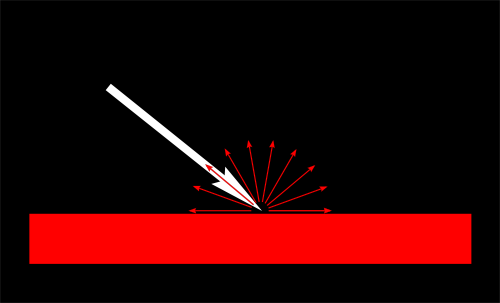
簡単な計算式でこれを実現できます。

color = MaterialDiffuseColor * LightColor * cosTheta;

光のモデル化

ろうそくのように空間の全方向に放出されるような光であると仮定します。

そのような光の場合、表面に到達する光束は光との距離に依存します。つまり遠くでは少ない光しか届きません。実際、光の量は距離の2乗で少なくなります。

color = MaterialDiffuseColor * LightColor * cosTheta / (distance*distance);

最後に、光の強さを調節するようなパラメータも必要です。これはLightColorにエンコードされます。(後のチュートリアルで見ます。)しかし、ここではただ色(例えば白色)と強さ(例えば60ワット)を持っていることとします。

color = MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance);

すべてを合わせる

このコードを動かすには、いくつかのパラメータ(色や強さ)とコードが必要です。

MaterialDiffuseColorは単純にテクスチャから取り出します。

LightColorとLightPowerはGLSL uniformを通してシェーダでセットします。

cosThetaはnとlに依存します。どの空間でも表現できますが、ここではカメラ空間を選びます。なぜならカメラ空間だと光の位置を計算するのが簡単だからです。

// カメラ空間で、計算されたフラグメントの法線
 vec3 n = normalize( Normal_cameraspace );
 // 光の方向(フラグメントから光の方向)
 vec3 l = normalize( LightDirection_cameraspace );

Normal_cameraspaceとLightDirection_cameraspaceは頂点シェーダで計算され、フラグメントシェーダへ送られます。

// クリップ空間での頂点の出力位置、MVP×位置
gl_Position =  MVP * vec4(vertexPosition_modelspace,1);

// ワールド空間での頂点の位置、M×位置
Position_worldspace = (M * vec4(vertexPosition_modelspace,1)).xyz;

// カメラ空間で、頂点からカメラへ向かうベクトル
// カメラ空間ではカメラは原点(0,0,0)にあります。
vec3 vertexPosition_cameraspace = ( V * M * vec4(vertexPosition_modelspace,1)).xyz;
EyeDirection_cameraspace = vec3(0,0,0) - vertexPosition_cameraspace;

// カメラ空間で、頂点から光へ向かうベクトル。Mは単位行列なので除外します。
vec3 LightPosition_cameraspace = ( V * vec4(LightPosition_worldspace,1)).xyz;
LightDirection_cameraspace = LightPosition_cameraspace + EyeDirection_cameraspace;

// カメラ空間での、頂点の法線
Normal_cameraspace = ( V * M * vec4(vertexNormal_modelspace,0)).xyz; // Only correct if ModelMatrix does not scale the model ! Use its inverse transpose if not.

このコードは難しそうに見えますが、チュートリアル3で習ったこと以外は使っていません。各ベクトルの名前に空間の名前が入れるように注意しました。だから、何が起こっているかを追っていくのがより簡単になります。あなたもそういう記法を取るべきです。

MとVはモデル行列とビュー行列で、MVP行列と同じようにシェーダへ送られます。

実行

拡散光を実装する上で必要となる情報はすべて出ました。やってみて、苦労しながら学びましょう。 :)

結果

拡散光要素のみで、次のような結果を得ます。(またまたひどいテクスチャですみません。)

前よりはよくなりましたが、まだ足りないものがあります。特に、clamp()を使ったのでスザンヌの後ろ側が真っ黒です。

環境光

環境光ではずるをします。

スザンヌの後ろ側はもう少し明るくなることを期待しています。なぜなら実生活ではランプは壁の後ろも照らすからです。それは物体の後ろ側を(より少ない)光で照らしています。

これを計算するには計算コストが高すぎます。

だから一般的な方法は単純に光を偽装します。実は、3Dモデルの後ろ側が真っ黒にならないようにするために、単純に3Dモデルに発光させるだけです。

これは次のように実現できます。

vec3 MaterialAmbientColor = vec3(0.1,0.1,0.1) * MaterialDiffuseColor;

color =
 // 環境光：直接当たらない光をシミュレートします。
 MaterialAmbientColor +
 // 拡散光：物体の"色"
 MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) ;

どうなったか見てみましょう。

結果

OK、少しよくなりました。より良い結果を得るために(0.1, 0.1, 0.1)を調整するのもよいでしょう。

鏡面光

反射する光のほかの部分は表面の光の反射する方向へ大部分反射します。これが鏡面光です。

画像で見たように、葉のような形をしています。極端なケースでは、拡散光はなくその葉はとても狭い範囲で(すべての光は一つの方向へ反射し)鏡のようになります。

(鏡を得るためにパラメータを微調整することも出来ますが、ここでは、この鏡で考慮すべきことはランプだけです。だから風変わりな鏡のようになります。)

// アイ(目)ベクトル(カメラのほうへ向かう)
vec3 E = normalize(EyeDirection_cameraspace);
// 三角形が光を反射する方向
vec3 R = reflect(-l,n);
// アイベクトルと反射ベクトルの間の角度のコサイン
// 0以上に固定します。
//  - 反射する方向を向いている -> 1
//  - 他の方向を見ている -> < 1
float cosAlpha = clamp( dot( E,R ), 0,1 );

color =
    // 環境光：直接当たらない光をシミュレートします。
    MaterialAmbientColor +
    // 拡散光：物体の"色"
    MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) ;
    // 鏡面光：鏡のように反射したハイライト
    MaterialSpecularColor * LightColor * LightPower * pow(cosAlpha,5) / (distance*distance);

Rは光が反射する方向です。Eは目の方向とは逆です。(“l”と同じです。)もし二つの角度が小さければ、反射する方向を見ていることを意味します。

pow(cosAlpha,5)は反射する”葉”の広さを調整するために使います。薄い”葉”を得るために5乗しています。

Final result

鼻や眉の鏡面光のハイライトに注目してください。

このシェーディングモデルは長い間簡単化のために使われてきました。しかし、これには多くの問題があります。だからmicrofacet BRDFのような物理ベースのモデルに置き換えられます。しかし、それは後のチュートリアルで見ます。

次のチュートリアルでは、VBOの性能を向上させる方法を学びます。これがはじめての中級編のチュートリアルです！