• インターフェース
• 実際のコード
  • 方向
  • 位置
  • 視野
  • 行列の計算
• 結果
  • バックフェースカリング
• 演習

6回目のチュートリアルにようこそ！

キーボードとマウスを使って、FPSのようにカメラを動かす方法を学びます。

インターフェース

このコードはチュートリアルを通して使うので、別のファイルで保存します。ファイルはcommon/controls.cppにあります。またtutorial06.cppにそれらを知らせるために、common/controls.hppで関数を宣言しておきます。

tutorial06.cppのコードは前のチュートリアルからあまり変えません。大きな変更点は、MVP行列を一度計算するのではなく、毎フレーム計算する必要がある点です。だからこのコードをメインループ内に移しましょう。

do{

    // ...

    // キーボードとマウスのインプットからMVP行列を計算する
    computeMatricesFromInputs();
    glm::mat4 ProjectionMatrix = getProjectionMatrix();
    glm::mat4 ViewMatrix = getViewMatrix();
    glm::mat4 ModelMatrix = glm::mat4(1.0);
    glm::mat4 MVP = ProjectionMatrix * ViewMatrix * ModelMatrix;

    // ...
}

このコードには3つの新しい関数があります。

• computeMatricesFromInputs()はキーボードとマウスを読み込み、射影行列とビュー行列を計算します。この関数が手品のタネです。
• getProjectionMatrix()は射影行列を返します。
• getViewMatrix()ビュー行列を返します。

もちろん、これは実現方法の一つに過ぎません。もし気に入らなければ、ソースコードを変更してください。

controls.cpp内で何が起きているのか見ていきましょう。

実際のコード

いくつかの変数が必要となります。

// 位置
glm::vec3 position = glm::vec3( 0, 0, 5 );
// 水平角、-Z方向
float horizontalAngle = 3.14f;
// 鉛直角、0、水平線を眺めている
float verticalAngle = 0.0f;
// 初期視野
float initialFoV = 45.0f;

float speed = 3.0f; // 3 units / second
float mouseSpeed = 0.005f;

FoVはズームレベルです。80°= 超広角,大きなゆがみがあります。60°-45°は一般的です。20°はすごいズームです。

最初にインプットに応じて位置、水平角、鉛直角と視野を再計算します。そして、その情報を元にビュー行列と射影行列を計算します。

方向

マウスの位置を読み込むのは簡単です。

// マウスの位置を取得します。
int xpos, ypos;
glfwGetMousePos(&xpos, &ypos);

一方で、マウスをスクリーンの中心に戻すときには注意が必要です。そうしなければ、すぐにウィンドウの外に出てしまい、それ以上動かせなくなってしまいます。

// 次のフレームのためにマウス位置をリセットします。
glfwSetMousePos(1024/2, 768/2);

このコードはウィンドウサイズを1024×768と仮定しています。もちろんこのサイズでなくても良いです。必要ならばglfwGetWindowSizeを使っても良いです。

これで視野角を計算できます。

// 新たな方向を計算します。
horizontalAngle += mouseSpeed * deltaTime * float(1024/2 - xpos );
verticalAngle   += mouseSpeed * deltaTime * float( 768/2 - ypos );

右から左に読んでみましょう。

• 1024/2 - xpos はマウスがウィンドウの中心からどの程度離れているかを意味します。この値が大きいほど、より動かしたいということを意味します。
• float(…) は計算がうまくいくようにfloat型に変換しています。
• mouseSpeed は回転の速度を速めたり遅くしたりするためにあります。好きなように調整してください。あるいはユーザに選ばせるのもありです。
• += マウスを動かさなければ 1024/2-xpos は0で、水平角は +=0 となり、水平角は変わりません。もし”+=”の代わりに”=”を使うと、毎フレーム、元の方向に戻ることになります。これはよくありません。

これで、ワールド空間でどちらの方向を向いているかを表現するベクトルを計算できます。

// 方向：球面座標から直角座標に変換します。
glm::vec3 direction(
    cos(verticalAngle) * sin(horizontalAngle),
    sin(verticalAngle),
    cos(verticalAngle) * cos(horizontalAngle)
);

これは一般的な計算です。コサインとサインを知らないならば、ここに簡単な説明を示します。

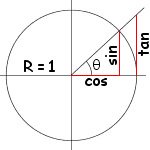上の式は3Dへの一般化です。

今”上”ベクトルを計算したいです。気をつけてほしいのは”上”は常に+Y方向ではないということです。もし下を向いているならば”上”方向は水平方向となります。これが同じ位置にあり、同じターゲットで、しかし違う”上”方向のカメラの例です。

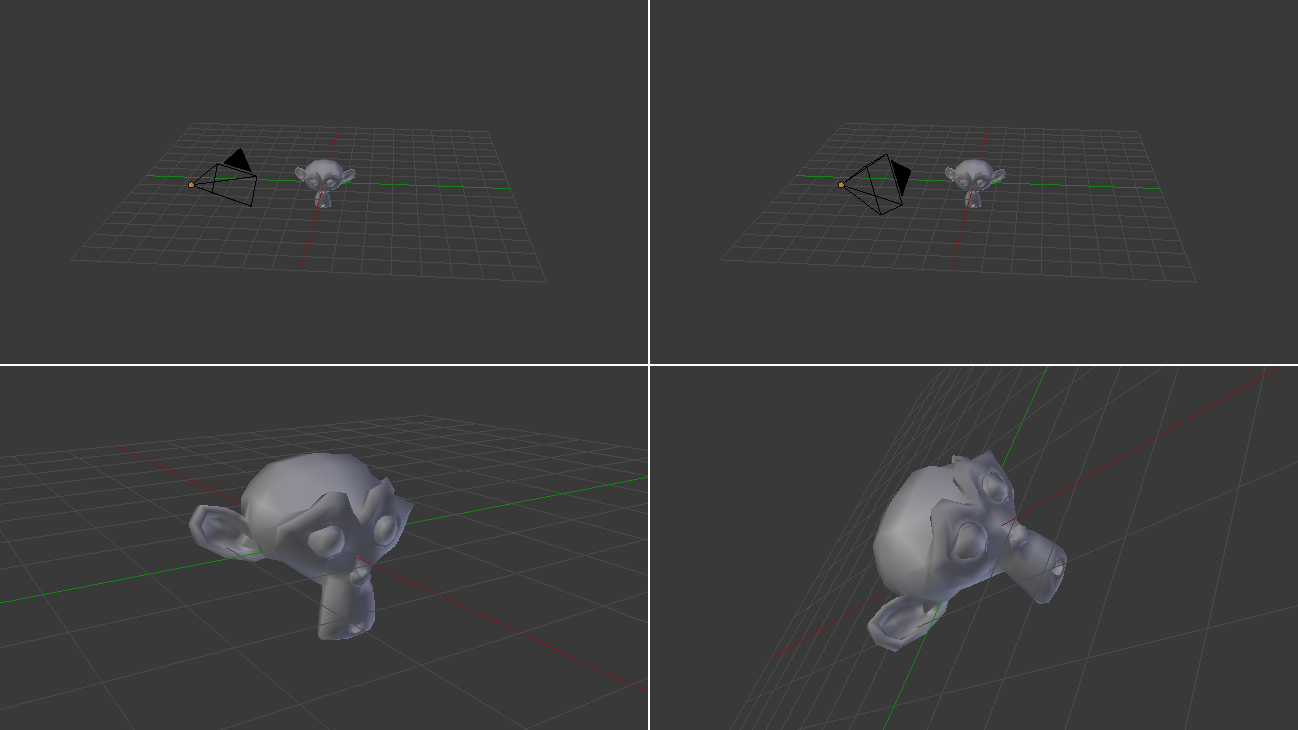
私たちのケースでは、カメラの右方向へ向かうベクトルは常に水平、ということは変化しません腕を水平にして、上や下やいろんな角度を見ることで、これを確認できるでしょう。だから”右”ベクトルを次のように定義しましょう。そのベクトルは水平なのでY座標は0で、XとYは上で示したような感じです。ただし、角度は90°あるいはPi/2ラジアンずつ回転しています。

// 右ベクトル
glm::vec3 right = glm::vec3(
    sin(horizontalAngle - 3.14f/2.0f),
    0,
    cos(horizontalAngle - 3.14f/2.0f)
);

これで”右”ベクトルと”方向・前”ベクトルを持っていることになります。”上”ベクトルはこれら2つのベクトルに垂直です。外積という便利な数学ツールで簡単に計算できます。

// 上ベクトル：右と前ベクトルに垂直
glm::vec3 up = glm::cross( right, direction );

外積が何をやっているか思い出してください。とてもシンプルなことを行っています。チュートリアル3の右手の法則を思い出してください。最初のベクトルは親指、2つ目は人差し指、結果は中指です。とっても便利でしょ？

位置

コードはとても簡単です。ところで、a/w/s/dキーの代わりに上/下/右/左キーを使います。なぜなら私のキーボードはazertyなので、a/w/s/dの位置ははz/q/s/dだからです。また韓国で使われているqwerZキーボードもまた配置が異なります。実のところ韓国人がどんなキーボードを使っているかは知りませんが、たぶんawsdとは違う配置のものを使っているでしょう。

// 前へ動きます。
if (glfwGetKey( GLFW_KEY_UP ) == GLFW_PRESS){
    position += direction * deltaTime * speed;
}
// 後ろへ動きます。
if (glfwGetKey( GLFW_KEY_DOWN ) == GLFW_PRESS){
    position -= direction * deltaTime * speed;
}
// 前を向いたまま、右へ平行移動します。
if (glfwGetKey( GLFW_KEY_RIGHT ) == GLFW_PRESS){
    position += right * deltaTime * speed;
}
// 前を向いたまま、左へ平行移動します。
if (glfwGetKey( GLFW_KEY_LEFT ) == GLFW_PRESS){
    position -= right * deltaTime * speed;
}

ここで特別なものはdeltaTimeです。次のような理由から、各フレームに1単位だけ動くのはあまり好ましくないでしょう。

• 60fpsで動くような早いコンピュータを使っていると、1秒で60×speedだけ動きます。
• 20fpsで動くような遅いコンピュータを使っていると、1秒で20×speedだけ動きます。

早いコンピュータだからといって早く移動させるわけではないので、”前のフレームからの時間”あるいは”時間差”で距離をスケーリングする必要があります。

• 60fpsで動くような早いコンピュータを使っていると、1フレームで1/60×speed単位だけ動きます。だから1秒で1×speedだけ動きます。
• 20fpsで動くような遅いコンピュータを使っていると、1フレームで1/20×speed単位だけ動きます。だから1秒で1×speedだけ動きます。.

こうするほうが好ましいでしょう。また、deltaTimeは簡単に計算できます。

double currentTime = glfwGetTime();
float deltaTime = float(currentTime - lastTime);

視野

よりおもしろくするために、マウスのホイールを視野に割り当てましょう。これにより安っぽいズーム機能を付けられます。

float FoV = initialFoV - 5 * glfwGetMouseWheel();

行列の計算

行列を計算するのは簡単です。以前とは違うパラメータを使って、前と同じような関数を使います。

// 射影行列：視野45°、4:3比、描画範囲0.1単位100単位
ProjectionMatrix = glm::perspective(glm::radians(FoV), 4.0f / 3.0f, 0.1f, 100.0f);
// カメラ行列
ViewMatrix       = glm::lookAt(
    position,           // カメラの位置
    position+direction, // 目標地点
    up                  // 上方向 (0,-1,0にセットすると上下逆さまになります。)
);

結果

バックフェースカリング

これで自由に動かせます。ただし、立方体の中へ移動しても、ポリゴンは表示されたままだということに気づくでしょう。これは明らかなように思えますが、この現象は最適化の絶好の機会です。実際、通常のアプリケーションでは立方体の中には決して移動しません。

カメラが三角形の後ろあるいは前にいるかどうかをGPUにチェックさせるというアイディアがあります。もし前にいれば三角形を表示します。もし後ろいて、メッシュが閉じていて、メッシュの中にいなければ、他の三角形がその前にあります。そして早く動いていることを除けば、誰も何も気づかないでしょう。平均で2倍三角形を減らせます。

良いことに、これはとても簡単にチェックできます。GPUは三角形の法線を計算します。(外積を使います。思い出せますか？)そしてこの法線がカメラのほうに向いてるかそうでないかをチェックします。

残念なことに、これはコストがかかります。つまり三角形の向きは暗黙的です。もしバッファ内の二つの頂点をひっくり返すと、間違いに終わるでしょう。しかし少しの追加の仕事をさせる価値があります。しばしば、3Dモデラーでは”法線を逆さまに”をクリックする必要があります。(実はこれは頂点を逆さまにし、そして法線です。)そしてすべてうまくいきます。

バックフェースカリングを有効にするのは簡単です。

// カメラのほうを向いていない法線の三角形をカリングします。
glEnable(GL_CULL_FACE);

演習

• 上下に移動できないようにverticalAngleを制限してください。
• オブジェクトの周りを回るようなカメラを作ってください。( position = ObjectCenter + ( radius * cos(time), height, radius * sin(time) ) )そして、radius/height/timeをキーボード/マウスなどにバインドします。
• 楽しんで！