• 同次座標
• 変換行列
  • 行列入門
  • 平行移動行列
  • 単位行列
  • 拡大縮小行列
  • 回転行列
  • 変換の組み合わせ
• モデル行列、ビュー行列、射影行列
  • モデル行列
  • ビュー行列
  • 射影行列
  • 行列の組み合わせ：モデルビュー射影行列
• すべてを合わせる
• 演習

エンジンは船を動かさない。船はそこにあり、エンジンは船の周りで世界を動かす。

フューチュラマ

これが全体のたったひとつの最も重要なチュートリアルです。少なくとも8回は読んでください。

同次座標

これまで、3D頂点を(x,y,z)の3つ組としてのみ考えていました。ここでwを導入しましょう。すると(x,y,z,w)というベクトルを得ます。

こうする理由がもうすぐ分かるでしょう。ただしこれだけは覚えておいてください。

• w == 1 ならばベクトル(x,y,z,1)は空間での位置を表します。
• w == 0 ならばベクトル(x,y,z,0)は方向を表します。

(もっと言えば、ずっと覚えておいてください。)

これが作り出す違いは何でしょう？例えば回転では、何も変えません。点か方向を回転させるとき、同じ結果を得られます。しかし平行移動のとき(特定の方向に点を移動させるとき)は、状況が違ってきます。”方向を平行移動させる”とはどういう意味でしょう？まぁ、気にしないでください。

同次座標はこれら二つのケースを一つの数式で表すことを可能にします。

変換行列

行列入門

簡単に言いますと、行列は行と列の数があらかじめ決まっている、数字の配列です。例えば、2x3行列は次のようになります。

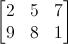
3Dグラフィックスでは、4x4の行列しか使いません。行列は頂点(x,y,z,w)を変換するときに役に立ちます。変換は頂点にと行列を掛け合わせることで実現します。

行列 x 頂点 (この順番！！) = 変換された頂点

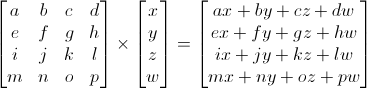
これは見た目ほどおっかなくありません。左手の指をaに、右手の指をxに乗せて下さい。これがaxです。左手の指を次の数字bに、右手の指を次の数字yにおいてください。するとbyを得ます。同様にcz、dwを得ます。つまりax + by + cz + dwとなります。これで新しいxを得ました！各行で同じことをやって下さい、すると新しい(x,y,z,w)が得られます。

この計算はとても退屈で、しかも頻繁に行います。そこで代わりにこれを計算してくれるように頼みましょう。

GLMを用いるC++：

glm::mat4 myMatrix;
glm::vec4 myVector;
// 何らかの方法でmyMatrixとmyVector満たす。
glm::vec4 transformedVector = myMatrix * myVector; // もう一度言いますが、この順番です！これは重要なことです。

** GLSL：**

mat4 myMatrix;
vec4 myVector;
// 何らかの方法でmyMatrixとmyVector満たす。
vec4 transformedVector = myMatrix * myVector; // そうです、GLMととても似ています。

( コードにこれをコピー＆ペーストしましたか？やってみましょう。)

平行移動行列

ここに理解するための最も簡単な平行移動行列を用意しました。平行移動行列は次のように表せます。

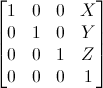
X、Y、Zは位置に加えたい値です。

だからベクトル(10,10,10,1)をX方向に10だけ平行移動させたいなら、次のように書けます。：

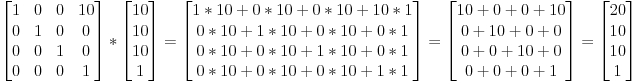
(計算してみましょう！絶対にやりましょう。)

…そして新たな同次ベクトル(20,10,10,1)が得られました！1というのは方向ではなく位置を表すことを思い出してください。だから変換によって位置を扱っているというという事実は変わりません。これは良いことです。

それでは-z軸方向を向いているベクトルに対しては何が起こるか見てみましょう。(0,0,-1,0)：

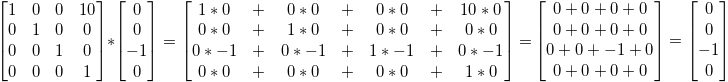
…つまりもとの(0,0,-1,0)方向は、上で言ったように、方向を動かすというのは何の意味もありません。

それでは、これをコードで実現するにはどうすれば良いでしょうか？

GLMを用いるC++：

#include <glm/gtx/transform.hpp> // <glm/glm.hpp>の後

glm::mat4 myMatrix = glm::translate(glm::mat4(), glm::vec3(10.0f, 0.0f, 0.0f));
glm::vec4 myVector(10.0f, 10.0f, 10.0f, 0.0f);
glm::vec4 transformedVector = myMatrix * myVector; // guess the result

**GLSL； **実は、GLSLではこのようにはできません。ほとんどの場合、行列を計算するためにC++でglm::translate()を使い、行列をGLSLに送り、掛け算をするだけです。

vec4 transformedVector = myMatrix * myVector;

単位行列

これは特別な行列です。何もしない行列です。しかし、これはA x 1.0がAとなることを知っているのと同じくらい重要なのでここで述べておきます。

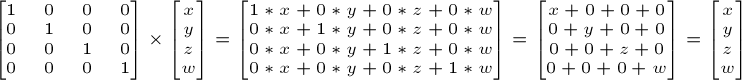
C++：

glm::mat4 myIdentityMatrix = glm::mat4(1.0f);

拡大縮小行列

拡大縮小行列も簡単です。

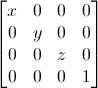
ここで全方向に2.0だけベクトル(位置でも方向でもどちらでも)を拡大したいならば次のようにやります。

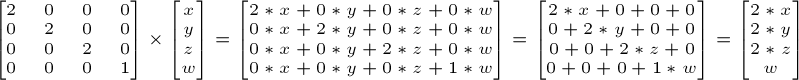
やはりwは変わりません。”方向を拡大(縮小)する”とはどういう意味か聞きたいかもしれません。えーと、まぁ聞かないでください。だから普通はこういうことはやりません。ただ一部のケースではとても便利に使えます。 (単位行列は拡大縮小行列の特別な場合です。つまり(X,Y,Z) = (1,1,1)です。また単位行列は平行移動行列の特別な場合でもあります。つまり(X,Y,Z) = (0,0,0)です。)

C++；

// #include <glm/gtc/matrix_transform.hpp> と #include <glm/gtx/transform.hpp>を使います。
glm::mat4 myScalingMatrix = glm::scale(2.0f, 2.0f ,2.0f);

回転行列

これらはとても複雑です。ここでは詳細は省きます。本当のレイアウトを知るのは、普通に使う上ではそれほど重要ではないからです。もっと知りたければMatrices and Quaternions FAQを見てください。(人気のページです。あなたの言語でもたぶん利用可能でしょう。)

C++：

// #include <glm/gtc/matrix_transform.hpp> と #include <glm/gtx/transform.hpp>を使います。
glm::vec3 myRotationAxis( ??, ??, ??);
glm::rotate( angle_in_degrees, myRotationAxis );

変換の組み合わせ

ここまででベクトルを回転、平行移動、拡大縮小する方法を学びました。これらの変換は組み合わせることができます。行列をお互いに掛けることによって実現します。例えば次のようになります。：

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;

！！！ 注意 ！！！ この行は、最初に拡大縮小、次に回転、最後に平行移動です。このようにして行列の掛け算は働きます。

違う順番で掛け合わせても同じ結果になるとは限りません。自分で確認してみましょう。：

• 前に進めてから左に回転する。
• 回転させてから前に進む。

実は、上の順番はゲームキャラクターや他のアイテムで通常必要とするものです。必要ならば最初に拡大縮小し、次に方向を決め、そして平行移動する。例えば、船モデルを考えましょう。(回転は簡単化のため省きます。)

• 間違ったやり方：

• (10,0,0)だけ船を平行移動させる。今、船の中心は原点から10だけ動きました。

• 船の大きさを2倍にします。現原点に比例してすべての方向が2倍されます。遠くに行ってしまった…最終的には大きな船を得ました。しかし中心は2*10 = 20です。これではだめでしょう。

• 正しいやり方：

• 船を2倍しましょう。すると中心が原点の大きな船を得ます。
• 船を平行移動させましょう。同じ大きさで、正しい距離だけ動きました。

行列と行列の掛け算は行列とベクトルの掛け算に良く似ています。だからここでは詳細を省きます。詳しくはMatrices and Quaternions FAQを見てください。それで、コンピュータに次のように頼めばやってくれます。：

GLMを用いたC++：

glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;

GLSL：

mat4 transform = mat2 * mat1;
vec4 out_vec = transform * in_vec;

モデル行列、ビュー行列、射影行列

以降のこのチュートリアルでは、Blenderの人気の3Dモデル、モンキースザンヌ、を描画する方法を知っていると仮定します。

モデル行列、ビュー行列、射影行列は変換をきれいに分けるための便利なツールです。これを使わないかもしれません。(実際、チュートリアル1と2では使いませんでした。)しかし、使うべきです。これがみんながやっている方法です。なぜなら、これから見ていくように、すべてをきれいに分けられるからです。

モデル行列

このモデルは、愛すべき私たちの三角形と同様に、頂点のセットで定義されています。これらの頂点のX、Y、Z座標はオブジェクトの中心の相対座標で定義されています。つまり、頂点(0,0,0)はオブジェクトの中心を表します。

ユーザがキーボードやマウスでモデルを動かせるようにしたいです。簡単です、既に習ってることをやればいいんです。平行移動回転拡大縮小です。各フレームごとに各頂点に対してこの行列を(C++ではなくGLSLで)適用すれば、すべてが動きます。ただし、_世界の中心_は動きません。

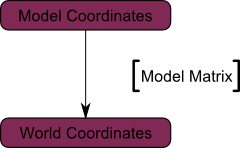
各頂点は今ワールド空間にあります。これは下の画像の黒い矢印が表しています。つまり私たちはモデル空間(すべての頂点がモデルの中心の相対座標で表される)からワールド空間(すべての頂点が世界の中心の相対座標で表される)へ移ったことになります。

これは下の図のように表せます。

ビュー行列

フューチュラマをもう一度引用しましょう。：

Tエンジンは船を動かさない。船はそこにあり、エンジンは船の周りで世界を動かす。

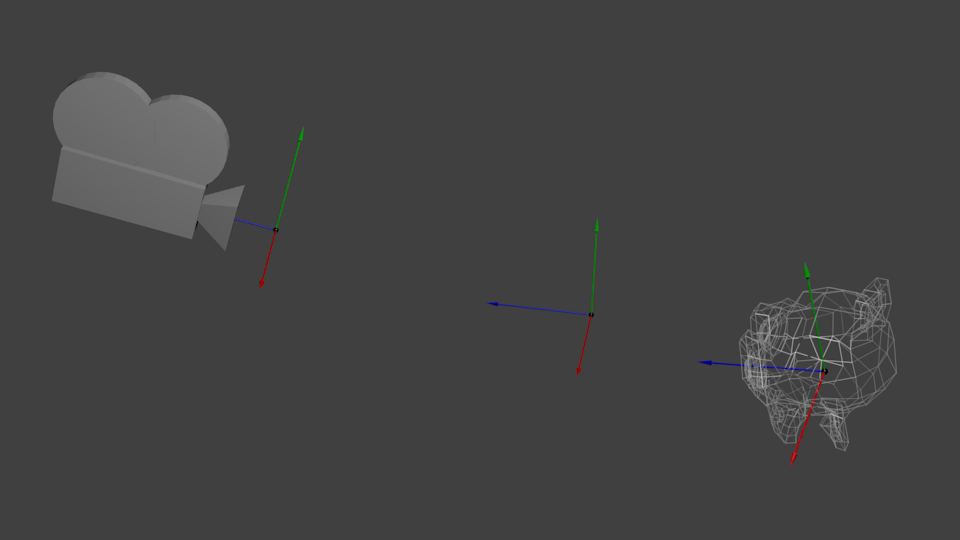
この考え方は、カメラにも適用できます。もし他の角度から山を見たいとき、カメラを動かすか…あるいは山を動かすことで実現できます。実際の世界では山を動かせませんが、コンピュータグラフィックの世界ではとてもシンプルで手軽にできます。

まずはじめに、カメラはワールド空間の原点にあります。世界を動かすためには、単純に行列を一つ導入すれば良いんです。それではカメラを右に3だけ(+X)動かしてみましょう。これは全世界(メッシュも含めて)を左に3だけ(-X)動かすことと同じです！混乱してるかもしれませんが、進みましょう。

// #include <glm/gtc/matrix_transform.hpp> と #include <glm/gtx/transform.hpp> を使います。
glm::mat4 ViewMatrix = glm::translate(glm::mat4(), glm::vec3(-3.0f, 0.0f, 0.0f));

再び、下の図がこの様子を表しています。私たちはワールド空間(前項で説明したように、すべての頂点が世界の中心の相対座標で表される)からカメラ空間(すべての頂点がカメラの相対座標で表される)へ移りました。

頭が爆発する前に、GLMのglm::LookAt関数を楽しんでください。

glm::mat4 CameraMatrix = glm::LookAt(
    cameraPosition, // ワールド空間でのカメラの位置
    cameraTarget,   // ワールド空間での見たい位置
    upVector        // たぶんglm::vec3(0,1,0)です。一方で(0,-1,0)にしたら上下逆さまになります。それもまた良いでしょう。
);

下の図のような感じになります。

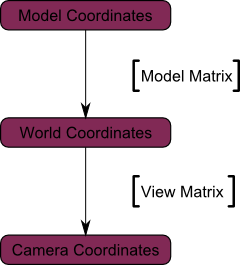
しかし、まだ終わっていません。

射影行列

私たちは今カメラ空間にいます。これは、これらの変換の後x==0とy==0である頂点はスクリーンの中心に描かれることを意味します。しかし、オブジェクトがスクリーンのどの位置に来るかを決定するのにxとy座標だけを使うわけではありません。つまりカメラからの距離zも使いたいんです！2つの頂点が同じxとyを持っているならば、より大きなz座標を持つ頂点を他の頂点よりもスクリーンの中心に置かれるでしょう。

これは透視投影法と呼ばれます。

幸運なことに、4x4行列はこの射影を表せます¹:

// 読むのが難しい行列を作ります。それでも、普通の標準の4x4行列です。
glm::mat4 projectionMatrix = glm::perspective(
    glm::radians(FoV), // 垂直方向のビューの広がり度合い（ラジアン）。つまり、"ズーム"の度合い。"カメラレンズ"を考えてください。通常90°(超ワイド) と 30° (とてもズームインしてる)の間です。
    4.0f / 3.0f,       // アスペクト比。ウィンドウのサイズに依存します。4/3 == 800/600 == 1280/960となっています。
    0.1f,              // 近くのクリッピング平面。できるだけ大きくします。そうしないと正確さの問題が出てくるでしょう。
    100.0f             // 遠くのクリッピング平面。できるだけ小さくします。
);

最後の一つです。

私たちはカメラ空間(すべての頂点がカメラの相対座標で表される)から同次空間(すべての頂点が小さな球の中で表される。球の中にある頂点がスクリーン上にある。)へ移りました。

そして、最後の説明図です。

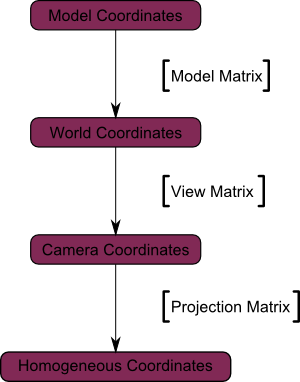
この射影でどんなことが起こったのかをより理解するために他の図を示します。射影の前、カメラ空間で、青いオブジェクトを得て、赤いところはカメラの四角錐台を表しています。つまり、カメラが実際に見ることのできるシーンの部分です。

すべてに射影行列を掛けると次のような効果があります。

この図では、今、四角錐台は完全な立方体となりました。(すべての軸が-1と1の間。それは少し見づらいです。)そして、青いオブジェクトは同じ方法で変形しました。そのため、カメラに近いオブジェクトは大きく(つまり私たちは見られない球の面に近い) 、他はより小さくなります。実世界と同じように！

四角錐台の後ろから、どのように見えるか見てみましょう。

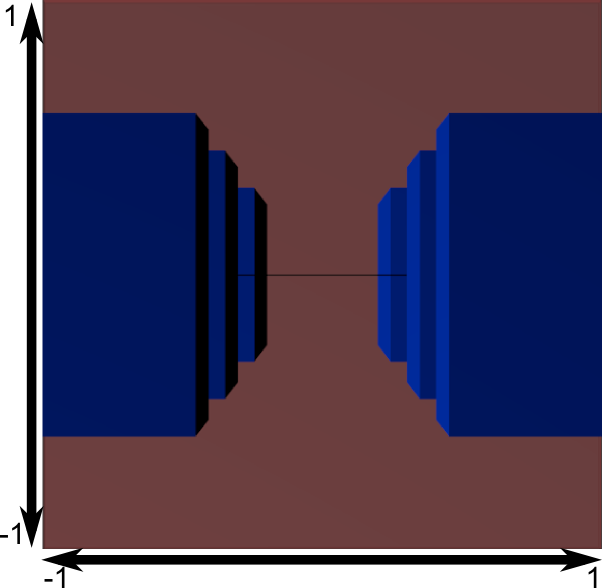
これで図が得られました！これは少し正方形すぎます。だから、実際のウィンドウサイズに合うように、他の数学変換を適用します。

そして、これが実際にレンダリングされる図です。

行列の組み合わせ：モデルビュー射影行列

… 既に慣れ親しんだ普通の行列の掛け算のようにやります！

// C++：行列を計算する。
glm::mat4 MVPmatrix = projection * view * model; // 逆になることを思い出して!

// GLSL：適用する
transformed_vertex = MVP * in_vertex;

すべてを合わせる

• ステップ1：MVP(ModelViewProjection)行列を作ります。レンダリングする各モデルごとに行います。

// 射影行列：45°の視界、アスペクト比4:3、表示範囲：0.1単位  100単位
glm::mat4 Projection = glm::perspective(glm::radians(45.0f), 4.0f / 3.0f, 0.1f, 100.0f);
// カメラ行列
glm::mat4 View       = glm::lookAt(
    glm::vec3(4,3,3), // ワールド空間でカメラは(4,3,3)にあります。
    glm::vec3(0,0,0), // 原点を見ています。
    glm::vec3(0,1,0)  // 頭が上方向(0,-1,0にセットすると上下逆転します。)
);
// モデル行列：単位行列(モデルは原点にあります。)
glm::mat4 Model      = glm::mat4(1.0f);  // 各モデルを変える！
// Our ModelViewProjection : multiplication of our 3 matrices
glm::mat4 MVP        = Projection * View * Model; // 行列の掛け算は逆になることを思い出してください。

• ステップ2：GLSLに渡します。

// "MVP" uniformへのハンドルを取得します。
// 初期化時だけ
GLuint MatrixID = glGetUniformLocation(programID, "MVP");

// 現在バインドしているシェーダの"MVP" uniformに変換を送る
// レンダリングする各モデルごと、なぜならMVPが違うからです。(少なくともMの部分が違います。)
glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &MVP[0][0]);

• ステップ3：頂点を変換させるためにGLSLで行列を使います。

in vec3 vertexPosition_modelspace;
uniform mat4 MVP;

void main(){

    // クリップ空間での、頂点のアウトプット位置：MVP * 位置
    vec4 v = vec4(vertexPosition_modelspace,1); // 同次4Dベクトルに変換します。覚えていますか？
    gl_Position = MVP * v;
}

• できました！チュートリアル2と同じ三角形ができました。原点は(0,0,0)ですが、(4,3,3,)から見て、(0,1,0)が上方向で、45°の視界です。

チュートリアル6ではゲームのようなカメラを作るためにキーボードやマウスを使った動的なこれらの値の修正方法を学びます。しかしまずは、3Dモデルでの色(チュートリアル4)とテクスチャ(チュートリアル5)の付け方を学びます。

演習

• glm::perspectiveを変えてみましょう。
• 透視投影変換の変わりに、平行投影(正射影)(glm::ortho)を使ってみましょう。
• モデル行列を三角形を平行移動、回転、拡大縮小の順になるように修正してみましょう。
• 同じものですが、違う順番で行ってみましょう。何か気づくことはありますか？キャラクターに使うならどの順番が”ベスト”でしょうか？

付録