Picking with custom Ray-OBB function
La dernière méthode est un sympathique compromis entre l’implémentation OpenGL « hacky » et l’utilisation d’un moteur physique complet pour de simples lancers de rayons.
Ce tutoriel utilise les concepts et les fonctions du tutoriel de Bullet, donc lis le avant celui-ci.
L’idée de base
Au lieu de dépendre de l’intersection d’un rayon contre une forme de collision dans Bullet, on va l’implémenter nous-mêmes.
Comme nous l’avons vu, il y a plusieurs formes de collision possibles. Les sphères sont très simples à intersecter, mais pour de nombreux objets, elles représentent très mal les modèles. D’un autre côté, l’intersection d’un rayon avec tous les triangles du modèle original est très couteuse. Les boîtes englobantes orientées (Oriented Bounding Box (OBB)) sont un bon compromis. Elles sont assez précises (mais cela dépend de tes géométries) et sont plutôt rapides à calculer.
Une OBB est une boîte englobant le modèle et lorsque le modèle est déplacé ou tourné, la même transformation est appliquée à la boîte :
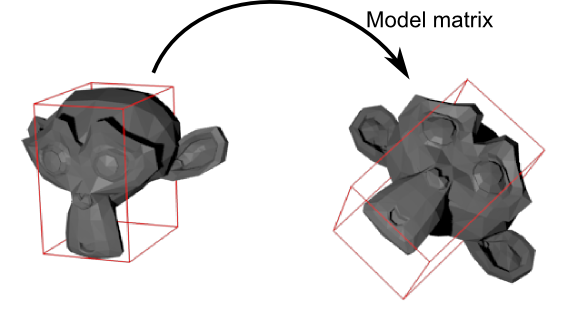
Algorithme d’intersection rayon-OBB
(L’algorithme et les figures s’inspirent grandement du livre Real-Time Rendering Vol. 3. Achete ce livre !)
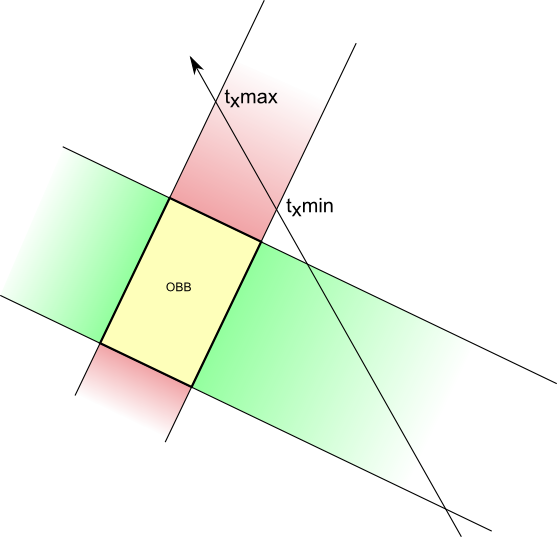
On a l’OBB ci-dessous. Sur l’axe des X, il est délimité par deux plans verticaux, ici en rouge. Lorsqu’ils sont intersectés par le rayon (une opération très simple), cela donne deux intersections, une « proche » et une « lointaine » :
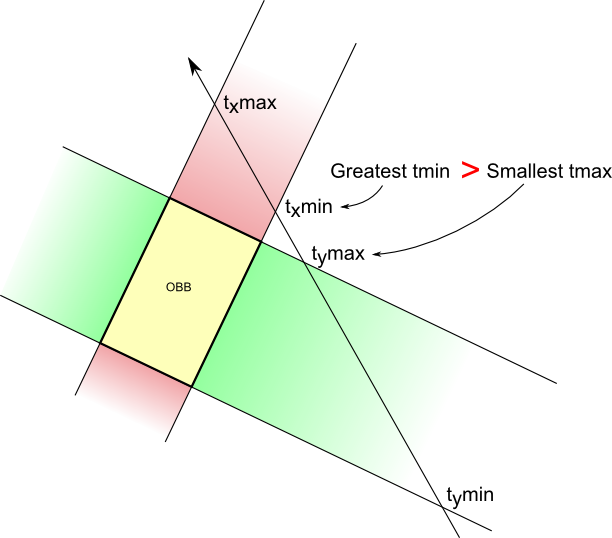
Lorsque le rayon intersecte les deux autres plans qui délimitent l’axe Y (en vert), cela donne deux intersections supplémentaires. Remarque comment les intersections sont ordonnées : tu entres dans la zone verte -> tu sors de la zone verte -> tu entres dans la zone rouge -> tu sors de la zone rouge. Cela signifie qu’il n’y a pas d’intersection.
Mais si l’ordre change (tu entres dans la zone verte -> tu entres dans la zone rouge), alors tu sais qu’il y a une intersection !
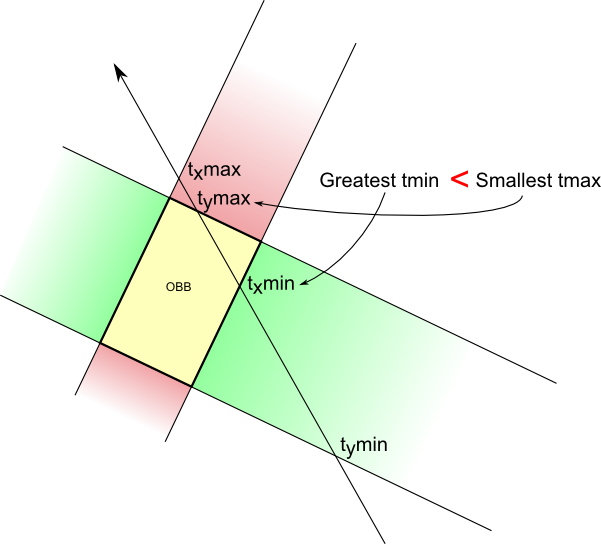
Mettons ça en pratique.
Implémentation de l’algorithme
(Le code complet est disponible dans le fichier Misc05/misc05_picking_custom.cpp)
Notre fonction d’intersection rayon - OBB ressemblera à cela :
bool TestRayOBBIntersection(
glm::vec3 ray_origin, // Origine du rayon, dans le repère du monde
glm::vec3 ray_direction, // Direction du rayon (PAS la cible !), dans le repère du monde. Doit être normalisé
glm::vec3 aabb_min, // Coordonnées minimales X,Y,Z du modèle lorsqu'il n'est pas transformé du tout
glm::vec3 aabb_max, // Coordonnées maximales X,Y,Z. Souvent aabb_min*-1 si votre modèle est centré, mais ce n'est pas toujours le cas
glm::mat4 ModelMatrix, // Transformation appliquée au modèle (et qui sera donc appliquée à la boîte englobante)
float& intersection_distance // Résultat : la distance entre ray_origin et l'intersection avec l'OBB
){
On commençe par initialiser quelques variables. tMin est la plus grande intersection « proche » actuellement trouvée ; tMax est la plus petite intersection « lointaine » trouvée jusqu’à présent. Delta est utilisé pour calculer les intersections avec les plans.
float tMin = 0.0f;
float tMax = 100000.0f;
glm::vec3 OBBposition_worldspace(ModelMatrix[3].x, ModelMatrix[3].y, ModelMatrix[3].z);
glm::vec3 delta = OBBposition_worldspace - ray_origin;
Maintenant, calculons l’intersection entre les deux plans qui délimitent l’OBB sur l’axe des X :
glm::vec3 xaxis(ModelMatrix[0].x, ModelMatrix[0].y, ModelMatrix[0].z);
float e = glm::dot(xaxis, delta);
float f = glm::dot(ray_direction, xaxis);
// Beware, don't do the division if f is near 0 ! See full source code for details.
float t1 = (e+aabb_min.x)/f; // Intersection with the "left" plane
float t2 = (e+aabb_max.x)/f; // Intersection with the "right" plane
t1 et t2 contiennent maintenant les distances entre l’origine du rayon et les intersections avec le plan, mais on ne sait pas dans quel ordre, donc on s’assure que t1 représente l’intersection « proche » et t2 l’intersection « lointaine » :
if (t1>t2){ // if wrong order
float w=t1;t1=t2;t2=w; // swap t1 and t2
}
On peut mettre à jour tMin et tMax :
// tMax est l'intersection « lointaine » la plus proche (parmi les paires de plans X,Y et Z)
if ( t2 < tMax ) tMax = t2;
// tMin est l'intersection « proche » la plus lointaine (parmi les paires de plans X,Y et Z)
if ( t1 > tMin ) tMin = t1;
Et voici une astuce : si l’intersection « lointaine » est plus proche que l’intersection « proche », il n’y a PAS d’intersection.
if (tMax < tMin )
return false;
Ça c’est pour l’axe des X. C’est exactement la même chose pour les autres axes !
Utiliser l’algorithme
La fonction TestRayOBBIntersections() permet de tester l’intersection avec une seule OBB, donc on doit toutes les tester. Dans ce tutoriel, on test simplement les boîtes les unes après les autres, mais si tu as plein d’objets, tu pourrais avoir besoin d’une structure accélératrice comme un arbre binaire de partitionnement de l’espace (Binary Space Partitionning Tree BSP-Tree) ou une hiérarchie de volume englobant (Bounding Volume Hierarchy BVH).
for(int i=0; i<100; i++){
float intersection_distance; // Output of TestRayOBBIntersection()
glm::vec3 aabb_min(-1.0f, -1.0f, -1.0f);
glm::vec3 aabb_max( 1.0f, 1.0f, 1.0f);
// The ModelMatrix transforms :
// - the mesh to its desired position and orientation
// - but also the AABB (defined with aabb_min and aabb_max) into an OBB
glm::mat4 RotationMatrix = glm::toMat4(orientations[i]);
glm::mat4 TranslationMatrix = translate(mat4(), positions[i]);
glm::mat4 ModelMatrix = TranslationMatrix * RotationMatrix;
if ( TestRayOBBIntersection(
ray_origin,
ray_direction,
aabb_min,
aabb_max,
ModelMatrix,
intersection_distance)
){
std::ostringstream oss;
oss << "mesh " << i;
message = oss.str();
break;
}
}
Remarque: cet algorithme a un problème ! il prend la première OBB qu’il trouve. Mais si cette OBB est derrière une autre, cela est faux. Donc tu dois prendre seulement l’OBB la plus proche ! C’est au lecteur de résoudre ce problème …
Avantages et inconvénients
Pros :
- Facile
- Nécessite peu de mémoire (seulement le surplus de l’OBB)
- Ne ralentit pas OpenGL comme le faisait la première version
Inconvénients :
- Plus lent qu’avec le moteur physique, car il n’y a pas de structure accélératrice
- Peut ne pas être assez précis
Remarques finales
Il y a de nombreuses autres routines d’intersection disponibles pour toutes sortes de formes de collisions ; lis par exemple http://www.realtimerendering.com/intersections.html.
Si tu as besoin d’une intersection précise, tu dois effectuer un test rayon-triangle. Encore une fois, ce n’est pas une bonne idée de vérifier tous les triangles de tous les modèles linéairement. Une structure accélératrice supplémentaire est nécessaire.