Tutoriel 8 : shaders de base
Dans ce huitième tutoriel, on va voir comment créer quelques shaders de base. Cela inclut :
- Obtenir un effet plus brillant lorsque l’on est plus proche de la source de lumière
- Obtenir une surbrillance lorsque l’on regarde le reflet d’une lumière (lumière spéculaire)
- Obtenir un effet plus sombre lorsque la lumière n’est pas directement devant le modèle (lumière diffuse) ;
- Enormément tricher (lumière ambiante).
Cela n’inclut pas :
- Les ombres : c’est un immense sujet nécessitant son(ses) propre(s) tutoriel(s)
- Les reflets similaires au miroir (incluant les reflets d’eau)
- N’importe quelle interaction sophistiquée avec la matière lumineuse comme le « subsurface scattering » (comme la cire)
- Les matériaux anisotropes (comme le métal brossé)
- Les shaders basés sur la physique, qui essaient d’imiter au mieux la réalité
- L’occlusion ambiante (il fait plus sombre dans une cave)
- Le mélange des couleurs (un tapis rouge fera qu’un plafond blanc sera un peu rouge)
- La transparence
- Tout genre d’illumination globale quelle qu’elle soit (c’est le nom regroupant toutes les techniques précédentes)
En un mot : simple.
Les normales
Au cours des tutoriels précédents tu as utilisé des normales sans vraiment savoir ce que c’est.
Les normales de triangle
La normale d’un plan est un vecteur de longueur 1 perpendiculaire à ce plan.
La normale d’un triangle est un vecteur de longueur 1 qui est perpendiculaire à ce triangle. Il est facilement calculé en utilisant le produit vectoriel de deux de ses côtés (le produit vectoriel de a et b produit un vecteur qui est perpendiculaire aux deux vecteurs a et b, tu te souviens ?), normalisé : sa longueur est ramenée à 1. En pseudo code :
triangle ( v1, v2, v3 )
edge1 = v2-v1
edge2 = v3-v1
triangle.normale = cross(edge1, edge2).normalize()
Ne mélange pas la normale et normalize(). normalize() divise un vecteur (n’importe quel vecteur et pas seulement une normale) par sa longueur afin que sa nouvelle longueur soit de 1. normale n’est qu’un nom pour quelques vecteurs qui représentent, eh bien, la normale.
Les normales de sommet
Par extension, on appelle la normale d’un sommet la combinaison des normales des triangles alentour. Cela est pratique car dans un vertex shader, on gère des sommets, donc c’est mieux d’avoir l’information sur le sommet. Et en aucun cas, on ne peut avoir d’informations sur les triangles en OpenGL. En pseudo code :
vertex v1, v2, v3, ....
triangle tr1, tr2, tr3 // all share vertex v1
v1.normal = normalize( tr1.normal + tr2.normal + tr3.normal )
Utiliser les normales de sommet en OpenGL
Pour utiliser les normales en OpenGL, c’est très simple. Une normale est un attribut de sommet, tout comme sa position, sa couleur, ses coordonnées UV… donc, on fait comme d’habitude. La fonction loadOBJ du septième tutoriel lit déjà les normales à partir du fichier OBJ.
GLuint normalbuffer;
glGenBuffers(1, &normalbuffer);
glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
glBufferData(GL_ARRAY_BUFFER, normals.size() * sizeof(glm::vec3), &normals[0], GL_STATIC_DRAW);
et
// 3rd attribute buffer : normals
glEnableVertexAttribArray(2);
glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
glVertexAttribPointer(
2, // attribute
3, // size
GL_FLOAT, // type
GL_FALSE, // normalized?
0, // stride
(void*)0 // array buffer offset
);
et c’est suffisant pour démarrer.
La partie diffuse
L’importance de la normale de la surface
Lorsque la lumière touche un objet, une importante partie de celle-ci est reflétée dans toutes les directions. C’est la composante « diffuse ». (On verra bientôt ce qui se passe avec l’autre partie.)
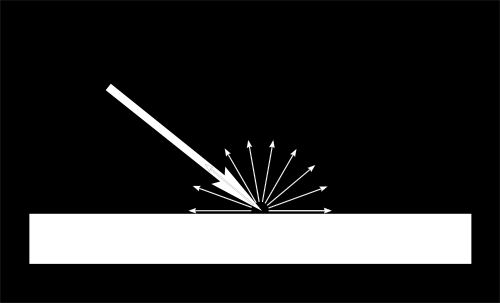
Lorsqu’un certain flux de lumière arrive sur la surface, la surface est illuminée différemment selon l’angle avec lequel la lumière arrive.
Si la lumière est perpendiculaire à la surface, elle est concentrée sur une petite surface. Si elle arrive de biais, la même quantité de lumière s’étale sur une plus grande surface :
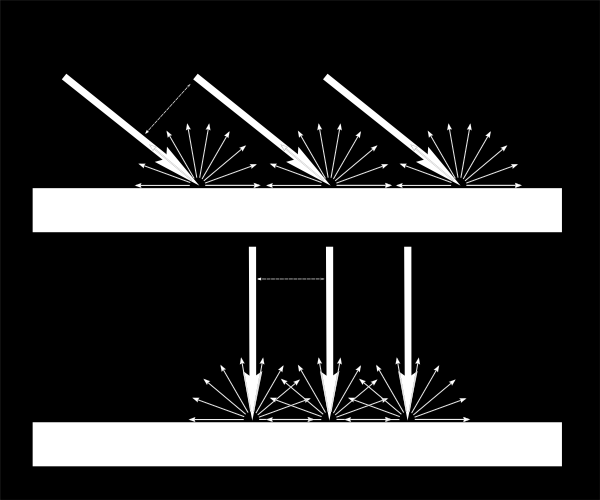
Cela signifie que chaque point de la surface sera plus sombre avec une lumière de biais (mais rappelez-vous, plus nombreux sont les points étant illuminés, donc la quantité de lumière totale reste la même).
Cela signifie que lorsque vous calculez la couleur d’un pixel, l’angle entre le rayon de lumière et la normale de la surface entre en jeu. Donc, on obtient :
// Cosine of the angle between the normal and the light direction,
// clamped above 0
// - light is at the vertical of the triangle -> 1
// - light is perpendicular to the triangle -> 0
float cosTheta = dot( n,l );
color = LightColor * cosTheta;
Dans ce code, n est la normale de la surface et l est le vecteur unitaire qui va de la surface vers la lumière (et non le contraire, même si ce n’est pas intuitif, cela rend les mathématiques plus simples).
Méfie toi du signe
Quelque chose manque dans la formule du cosTheta. Si la lumière est derrière le triangle, n et l seront opposés, donc n.l sera négatif. Cela signifie que la couleur aura une valeur négative, ce qui ne veut rien dire. Donc nous devons limiter cosTheta à 0 :
// Cosine of the angle between the normal and the light direction,
// clamped above 0
// - light is at the vertical of the triangle -> 1
// - light is perpendicular to the triangle -> 0
// - light is behind the triangle -> 0
float cosTheta = clamp( dot( n,l ), 0,1 );
color = LightColor * cosTheta;
Couleur de matériel
Bien sûr, la couleur de sortie dépend aussi de la couleur du matériel. Dans cette image, la lumière blanche est composée de lumière verte, rouge et bleue. Lors de la collision avec le matériel rouge, les lumières verte et bleue sont absorbées et seule la lumière rouge reste.
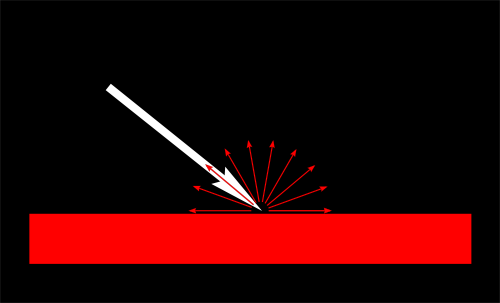
On peut modéliser cela par une simple multiplication :
color = MaterialDiffuseColor * LightColor * cosTheta;
Modéliser la lumière
Premièrement, on fera l’hypothèse que l’on a une lumière ponctuelle qui émet dans toutes les directions de l’espace, comme une bougie.
Avec une telle lumière, le flux lumineux que recevra la surface dépendra de sa distance avec la source de lumière : plus loin elle est, moins elle est illuminée. En fait, la lumière diminuera avec le carré de la distance :
color = MaterialDiffuseColor * LightColor * cosTheta / (distance*distance);
Enfin, on a besoin d’un autre paramètre pour contrôler la puissance de la lumière. Cela peut être ajouté à LightColor (et on le fera dans un prochain tutoriel), mais pour le moment utilisez deux variables : la couleur (par exemple, blanche) et la puissance (par exemple 60 watts).
color = MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance);
Combiner le tout
Pour que ce code fonctionne, on a besoin de plusieurs paramètres (les différentes couleurs et puissances) et d’un peu plus de code.
MaterialDiffuseColor est simplement récupéré à partir de la texture.
LightColor et LightPower sont définies dans le shader avec les variables uniformes GLSL.
cosTheta dépend de n et l. On peut les exprimer dans n’importe quel espace de coordonnées tant qu’il est le même pour les deux. On choisit l’espace caméra car c’est facile de calculer la position de la lumière dans cet espace :
// Normal of the computed fragment, in camera space
vec3 n = normalize( Normal_cameraspace );
// Direction of the light (from the fragment to the light)
vec3 l = normalize( LightDirection_cameraspace );
avec les variables Normal_cameraspace et LightDirection_cameraspace calculées dans le vertex shader et passées au fragment shader :
// Output position of the vertex, in clip space : MVP * position
gl_Position = MVP * vec4(vertexPosition_modelspace,1);
// Position of the vertex, in worldspace : M * position
Position_worldspace = (M * vec4(vertexPosition_modelspace,1)).xyz;
// Vector that goes from the vertex to the camera, in camera space.
// In camera space, the camera is at the origin (0,0,0).
vec3 vertexPosition_cameraspace = ( V * M * vec4(vertexPosition_modelspace,1)).xyz;
EyeDirection_cameraspace = vec3(0,0,0) - vertexPosition_cameraspace;
// Vector that goes from the vertex to the light, in camera space. M is ommited because it's identity.
vec3 LightPosition_cameraspace = ( V * vec4(LightPosition_worldspace,1)).xyz;
LightDirection_cameraspace = LightPosition_cameraspace + EyeDirection_cameraspace;
// Normal of the the vertex, in camera space
Normal_cameraspace = ( V * M * vec4(vertexNormal_modelspace,0)).xyz; // Only correct if ModelMatrix does not scale the model ! Use its inverse transpose if not.
Ce code peut sembler impressionnant mais il n’y a rien que l’on n’ait pas vu dans le troisième tutoriel : les matrices. J’ai fait attention d’écrire le nom de chaque espace dans le nom des vecteurs pour qu’il soit plus simple de garder trace de ce qui se passe. Tu devrais aussi faire ça.
M et V sont les matrices de Modèle et de Vue, qui sont passées aux shaders de la même façon que MVP.
C’est l’heure de bosser
Tu as tout ce qu’il faut pour coder la lumière diffuse. Vas-y et apprends à la dure :)
Résultat
Avec seulement la composante diffuse, on obtient le résultat suivant (désolé pour la texture moche encore une fois) :

C’est mieux qu’avant, mais c’est encore bien incomplet. En particulier, l’arrière de Suzanne est complètement noir car nous avons utilisé clamp().
La composante ambiante
La composante ambiante est la plus grande triche qui existe !
On s’attend à ce que le dos de Suzanne reçoive plus de lumière car, dans la vraie vie, la lampe éclairerait le mur derrière, ce qui éclairerait (pas mal moins) l’arrière de l’objet.
Ça serait affreusement coûteux à calculer.
Donc, l’astuce habituelle est de simplement imiter cette lumière. En fait, le modèle 3D va émettre de la lumière afin de ne pas apparaître complètement noir.
Cela peut être fait de cette façon :
vec3 MaterialAmbientColor = vec3(0.1,0.1,0.1) * MaterialDiffuseColor;
color =
// Ambient : simulates indirect lighting
MaterialAmbientColor +
// Diffuse : "color" of the object
MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) ;
Voyons ce que ça donne.
Résultat
Ok, donc c’est un petit peu mieux. Tu peux ajuster le (0.1, 0.1, 0.1) si tu souhaites un meilleur résultat.

La composante spéculaire
L’autre partie de la lumière qui est réfléchie l’est principalement dans la direction qui est le reflet de la source de lumière sur la surface. C’est la composante spéculaire.

Comme tu peux le voir dans cette image, cela forme une sorte de lobe. Dans les cas extrêmes, la composante diffuse peut être nulle, le lobe peut être très très étroit (toute la lumière est réfléchie dans une seule direction) et on obtient un miroir.
(on peut effectivement ajuster les paramètres pour obtenir un miroir mais, dans notre cas, la seule chose que l’on prend en compte dans ce miroir est la lampe. Donc, cela ferait un miroir très étrange.)
// Eye vector (towards the camera)
vec3 E = normalize(EyeDirection_cameraspace);
// Direction in which the triangle reflects the light
vec3 R = reflect(-l,n);
// Cosine of the angle between the Eye vector and the Reflect vector,
// clamped to 0
// - Looking into the reflection -> 1
// - Looking elsewhere -> < 1
float cosAlpha = clamp( dot( E,R ), 0,1 );
color =
// Ambient : simulates indirect lighting
MaterialAmbientColor +
// Diffuse : "color" of the object
MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) ;
// Specular : reflective highlight, like a mirror
MaterialSpecularColor * LightColor * LightPower * pow(cosAlpha,5) / (distance*distance);
R est la direction vers laquelle la lumière reflète. E la direction inverse de la vue (tout comme nous l’avons fait pour l) ; si l’angle entre ces deux vecteurs est petit, cela signifie que l’on regarde directement dans le reflet.
pow(cosAlpha,5) est utilisé pour contrôler la largeur du lobe de lumière spéculaire. Augmentez le 5 pour obtenir un lobe plus mince.
Résultat final

Remarque la surbrillance spéculaire sur le nez et les sourcils.
Ce modèle de shaders a été utilisé pendant des années de par sa simplicité. Il possède un grand nombre de problèmes, donc il est remplacé par des modèles basés sur la physique comme le BRDF à microfacettes, mais on verra cela plus tard.
Dans le prochain tutoriel, on apprendra à améliorer les performances de votre VBO. Cela sera le premier tutoriel intermédiaire !