• Coordonnées homogènes
• Matrices de transformation
  • Une introduction aux matrices
  • Matrices de translation
  • La matrice d’identité
  • Matrices de mise à l’échelle
  • Matrices de rotation
  • Combiner les transformations
• Les matrices de modèle, de vue et de projection
  • La matrice de modèle
  • La matrice de vue
  • La matrice de projection
  • Combiner des transformations : la matrice ModelViewProjection
• Mettre tout ensemble
• Exercices

Les moteurs ne déplacent pas du tout le vaisseau. Le vaisseau reste où il est et les moteurs déplacent l’univers autour de lui.

Futurama

C’est le tutoriel le plus important de tous. Tu devrais le garder en livre de chevet, et le lire et relire au moins 8 fois !

Coordonnées homogènes

Jusqu’à présent, on a considéré les sommets 3D comme des triplets (x, y, z). On va introduire w, ce qui donnera des vecteurs (x, y, z, w).

Cela deviendra bientôt clair, mais pour le moment, retiens ça :

• Si w == 1, alors le vecteur (x, y, z, 1) est une position dans l’espace.
• Si w == 0, alors le vecteur (x, y, z, 0) est une direction.

(En fait, retiens ça à vie.)

Quelle différence cela fait-il ? Eh bien, pour une rotation, ça change rien. Lorsque tu tournes un point ou une direction, tu obtiens le même résultat. Par contre, pour une translation (lorsque tu déplaces un point dans une certaine direction), les choses sont différentes. Que signifie « déplacer une direction » ? Pas grand-chose.

Les coordonnées homogènes permettent d’utiliser une simple formule mathématique pour gérer ces deux cas.

Matrices de transformation

Une introduction aux matrices

De façon simple, une matrice est un tableau de nombres avec un nombre prédéfini de lignes et colonnes. Par exemple, une matrice 2x3 ressemble à ceci :

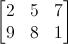
En programmation 3D, on utilise uniquement des matrices 4x4. Elles vont permettre de transformer les vecteurs (x, y, z, w). Cela s’effectue en multipliant le vertex (sommet) par la matrice :

Matrix x Sommet (dans cet ordre !!) = SommetTransformé

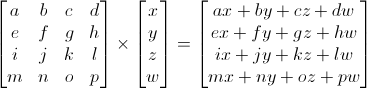
Ce n’est pas aussi effrayant qu’il y paraît. Place un doigt de ta main gauche sur le ‘a’ et un doigt de ta main droite sur le ‘x’. C’est ax. Déplace ta main gauche sur le prochain nombre (b) et ta main droite sur le prochain nombre (y). Tu obtiens by. Encore une fois : cz. Une nouvelle fois : dw. ax + by + cz + dw. Tu as ton nouveau ‘x’. Fais de même pour chaque ligne et tu obtiendras ton nouveau vecteur (x, y, z, w).

Comme c’est vraiment ennuyeux à calculer et qu’on va le faire souvent, on va laisser l’ordinateur le faire pour nous.

En C++, avec GLM :

glm::mat4 myMatrix;
glm::vec4 myVector;
// fill myMatrix and myVector somehow
glm::vec4 transformedVector = myMatrix * myVector; // Again, in this order ! this is important.

En GLSL :

mat4 myMatrix;
vec4 myVector;
// fill myMatrix and myVector somehow
vec4 transformedVector = myMatrix * myVector; // Yeah, it's pretty much the same than GLM

(as-tu copié-collé ça dans ton code ? Vas-y ! Essaye ! )

Matrices de translation

Ce sont les plus simples matrices de transformation à comprendre. Une matrice de translation ressemble à ça :

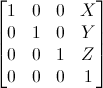
où X, Y, Z sont les valeurs que l’on souhaite ajouter à notre position.

Donc, si l’on veut déplacer le vecteur (10, 10, 10, 1) de dix unités sur l’axe des X, on obtient :

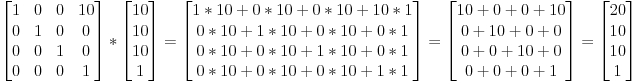
( Fais le calcul ! C’est vraiment important ! )

… et on obtient un vecteur homogène (20, 10, 10, 1) ! Rappelle-toi, le 1 signifie que c’est une position et non pas une direction. Donc notre transformation n’a pas modifié le fait que nous utilisons une position, ce qui est une bonne chose.

Voyons voir maintenant ce qui se passe pour un vecteur qui représente une direction vers l’axe -Z : (0, 0, -1, 0)

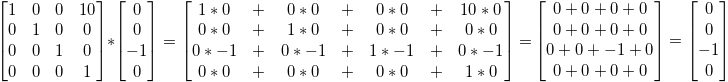
… soit, notre direction originale (0, 0, -1, 0), ce qui est juste, car comme on l’a dit précédemment, le déplacement d’une direction n’a aucun sens.

Donc, qu’est ce que ca donne dans le code ?

En C++, avec GLM :

#include <glm/gtx/transform.hpp> // after <glm/glm.hpp>
 
glm::mat4 myMatrix = glm::translate(glm::mat4(), glm::vec3(10.0f, 0.0f, 0.0f));
glm::vec4 myVector(10.0f, 10.0f, 10.0f, 0.0f);
glm::vec4 transformedVector = myMatrix * myVector; // guess the result

En GLSL : Bon, en fait, vous ne le ferez presque jamais. La plupart du temps, vous utilisez glm::translate() en C++ pour calculer votre matrice et vous l’envoyez au GLSL et vous la multipliez simplement par votre vecteur :

vec4 transformedVector = myMatrix * myVector;

La matrice d’identité

Celle-ci est spéciale. Elle ne fait rien. Mais on la mentionne car c’est important de pas oublier que A fois 1.0 donne A.

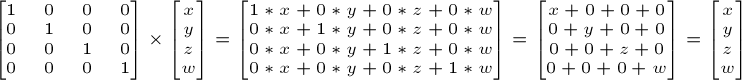
En C++ :

glm::mat4 myIdentityMatrix = glm::mat4(1.0f);

Matrices de mise à l’échelle

Les matrices de mise à l’échelle sont aussi assez simples :

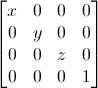
Donc si tu veux redimensionner un vecteur (une position ou une direction, peu importe) par 2.0 dans toutes les directions :

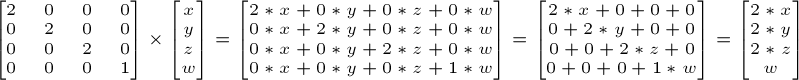
et la valeur de w ne change pas. Tu peux te demander : quel est le sens d’une mise à l’échelle d’une direction ? Eh bien, souvent, pas grand-chose. Généralement, on ne le fait pas sauf dans quelques (rares) cas où cela peut être pratique.

La matrice d’identité n’est qu’un cas spécifique des matrices de redimensionnement, avec (X, Y, Z) = (1, 1, 1). C’est aussi un cas spécifique des matrices de translation avec (X, Y, Z) = (0, 0, 0).

En C++ :

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 myScalingMatrix = glm::scale(2.0f, 2.0f ,2.0f);

Matrices de rotation

Elles sont assez compliquées. Je vais passer les détails ici, sachant qu’il n’est pas important de connaître leur fonctionnement pour un usage quotidien. Pour plus d’informations, jete un oeil à cette populaire FAQ sur les matrices et quaternions (en anglais). Tu peux aussi regarder le tutoriel sur les rotations.

En C++ :

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::vec3 myRotationAxis( ??, ??, ??);
glm::rotate( angle_in_degrees, myRotationAxis );

Combiner les transformations

Voilà, on sait comment tourner, déplacer et redimensionner nos vecteurs. Cela serait bien si on pouvait combiner ces transformations. C’est possible en multipliant les matrices ensemble, par exemple :

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;

!! ATTENTION !! Cette ligne effectue la mise à l’échelle en premier, puis la rotation, et finalement la translation. C’est ainsi que la multiplication de matrice fonctionne.

Le résultat serait différent en écrivant ces opérations dans un autre ordre. Teste-le toi-même :

• fais un pas en avant (attention à ton ordi) et tourne vers la gauche
• tourne vers la gauche et fais un pas en avant.

En fait, l’ordre utilisé ci-dessus est celui que l’on va utiliser pour les personnages et objets de ton jeu (ou application) : la mise à l’échelle en premier (si besoin) ; puis sa rotation ; finalement la translation. Par exemple, pour un vaisseau (pour simplifier, les rotations ont été retirées) :

• La mauvaise façon :
  • Tu déplaces le vaisseau de (10, 0, 0). Son centre est maintenant à dix unités de l’origine ;
  • Tu redimensionnes la taille de ton vaisseau d’un facteur 2. Toutes les coordonnées sont multipliées par 2 par rapport à l’origine, qui est très loin… finalement tu as un gros vaisseau, mais centré à 2*10 = 20. Chose que tu ne veux pas.
• La bonne façon :
  • Tu redimensionnes la taille de ton vaisseau d’un facteur 2. Tu obtiens un gros vaisseau, centré sur l’origine ;
  • Tu déplaces ton vaisseau. Il conserve la même taille et il est au bon endroit.

Les multiplications de matrices * matrices sont très proches des multiplications matrices * vecteur, donc encore une fois, je vais passer quelques détails et te rediriger vers la FAQ des matrices si nécessaire. Pour le moment, on demande simplement à l’ordinateur de le faire :

En C++, avec GLM :

glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;

En GLSL :

mat4 transform = mat2 * mat1;
vec4 out_vec = transform * in_vec;

Les matrices de modèle, de vue et de projection

Pour la suite du tutoriel, on supposera savoir comment dessiner le modèle 3D favori de Blender : le singe Suzanne. Même si c’est pas encore le cas

Les matrices de modèle, de vue et de projection sont des outils pratiques pour différencier proprement les transformations. Tu peux ne pas les utiliser (après tout, c’est ce que l’on a fait dans les deux premiers tutoriels). Mais tu devrais. C’est la façon que tout le monde utilise, car c’est une approche propre, comme on va le voir.

La matrice de modèle

Le modèle, tout comme notre triangle rouge adoré, est défini par un ensemble de sommets. Les coordonnées X, Y, Z de ces sommets sont définies par rapport au centre de l’objet : ce qui veut dire que si un vertex est en (0, 0, 0), il est au centre de l’objet.

On aimerait pouvoir déplacer cet objet, peut-être car le joueur le contrôle avec le clavier et la souris. Facile, on vient juste d’apprendre à le faire : déplacement * rotation * redimensionnement, et c’est fini ! On applique cette matrice sur tous nos sommets, à chaque fois qu’on dessine l’écran (en GLSL, pas en C++) et tout le modèle bouge. Quelque chose qui ne bouge pas sera au centre du monde.

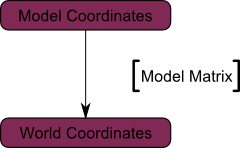
Nos sommets sont maintenant dans le repère du monde. C’est la signification de la flèche noire dans l’image ci-dessous : on s’est déplacé de l’espace du modèle (tous les sommets sont définis par rapport au centre du modèle) à l’espace monde (tous les sommets sont définis par rapport au centre du monde).

On peut résumer cela avec le diagramme suivant :

La matrice de vue

Voici une nouvelle fois la citation de Futurama :

Les moteurs ne déplacent pas du tout le vaisseau. Le vaisseau reste où il est et les moteurs déplacent l’univers autour de lui.

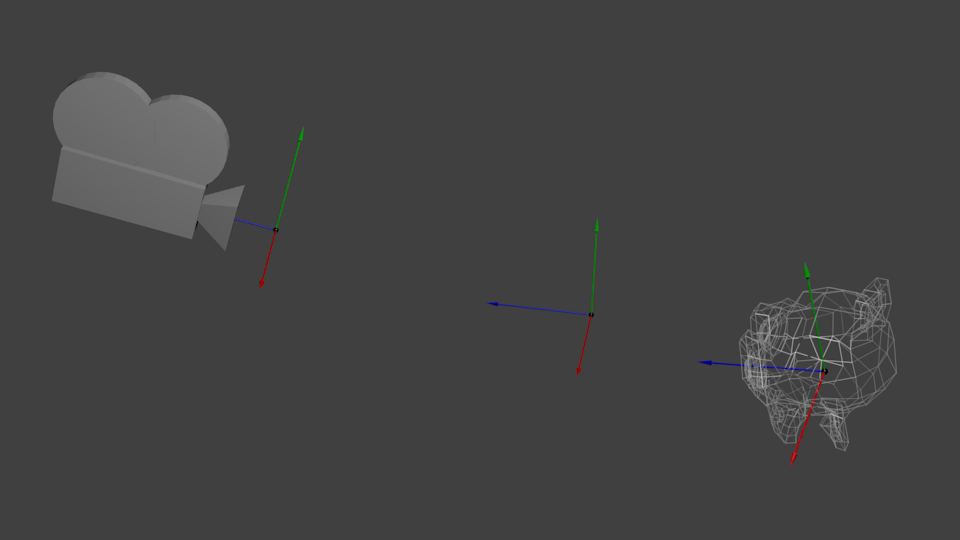
Lorsqu’on y pense, la même chose s’applique aux caméras. Si on souhaite voir une montagne à partir d’un autre angle, on peut déplacer soit la caméra… soit la montagne. Bien que cela ne soit pas possible dans la vraie vie, c’est très simple et pratique dans le monde de l’infographie.

Au début, notre caméra est à l’origine dans le _repère du monde. Afin de déplacer le monde, vous introduisez une nouvelle matrice, tout simplement. Imagine que tu veux déplacer la caméra de trois unités vers la droite (+X). C’est équivalent à déplacer l’ensemble du monde (les modèles inclus) trois unités sur la GAUCHE ! (-X). Pendant que ton cerveau fond, voici comment faire :

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 ViewMatrix = glm::translate(glm::mat4(), glm::vec3(-3.0f, 0.0f, 0.0f));

L’image ci-dessous illustre ce phénomène : on s’est déplacé du repère du monde (tous les sommets sont définis par rapport au centre du monde, comme on l’avait fait dans la section précédente) vers le repère de la caméra (tous les sommets sont définis par rapport à la caméra).

Avant que votre tête n’explose, admire cette superbe fonction glm::LookAt de GLM :

glm::mat4 CameraMatrix = glm::lookAt(
    cameraPosition, // the position of your camera, in world space
    cameraTarget,   // where you want to look at, in world space
    upVector        // probably glm::vec3(0,1,0), but (0,-1,0) would make you looking upside-down, which can be great too
);

Voici le diagramme obligatoire :

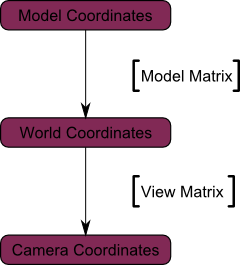
Ce n’est pas encore fini. C’est vrai que c’est beaucoup d’un coup, mais accroche-toi. T’y es presque !

La matrice de projection

On est maintenant dans le repère de la caméra. Cela signifie qu’après toutes ces transformations, un sommet ayant les coordonnées x == 0 et y == 0 devrait être affiché au centre de l’écran. Mais on ne peut pas utiliser uniquement les coordonnées x et y pour déterminer où un objet devrait être placé à l’écran : sa distance par rapport à la caméra (z) est aussi importante ! Pour deux sommets avec les mêmes coordonnées x et y, le sommet avec la plus grande coordonnée z sera plus au centre de l’écran que l’autre.

Cela s’appelle une projection de perspective :

Et heureusement pour nous, cette projection peut être représentée par une matrice 4x4¹ :

// Generates a really hard-to-read matrix, but a normal, standard 4x4 matrix nonetheless
glm::mat4 projectionMatrix = glm::perspective(
    glm::radians(FoV), // The vertical Field of View, in radians: the amount of "zoom". Think "camera lens". Usually between 90° (extra wide) and 30° (quite zoomed in)
    4.0f / 3.0f,       // Aspect Ratio. Depends on the size of your window. Notice that 4/3 == 800/600 == 1280/960, sounds familiar ?
    0.1f,              // Near clipping plane. Keep as big as possible, or you'll get precision issues.
    100.0f             // Far clipping plane. Keep as little as possible.
);

Une dernière fois :

On s’est déplacé du repère de la caméra (tous les sommets sont définis par rapport à la caméra) vers le repère homogène (tous les sommets sont définis dans un petit cube). Tout ce qui est dans le cube apparaîtra à l’écran.

Et voici le diagramme final :

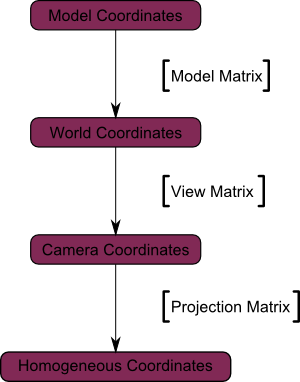
Voici un nouveau schéma afin que tu comprennes mieux ce qui se passe avec la projection. Avant la projection, on a les objets en bleu, dans le repère caméra, et la forme rouge représente le champ de la caméra : la partie de la scène que la caméra est capable de voir.

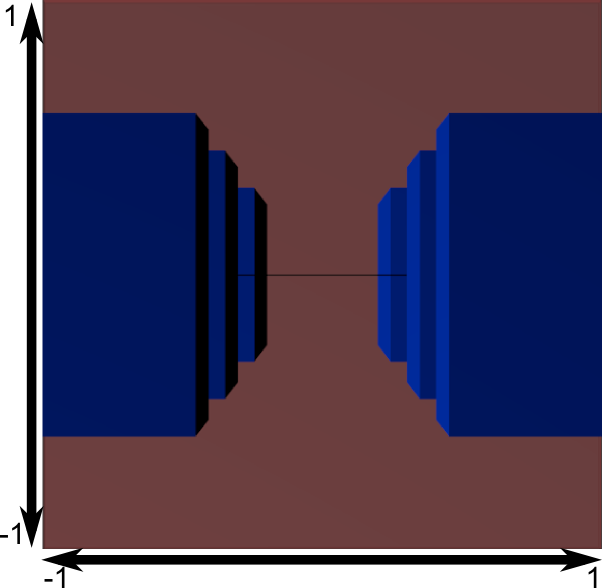
Et voici ce que l’on obtient en multipliant tout par la matrice de projection :

Dans cette image, le champ de la caméra (frustum en anglais) est devenu un cube parfait (entre -1 et 1 sur tous les axes, même si c’est un peu dur à voir) et tous les objets en bleu ont été déformés de la même façon. Donc, les objets proches de la caméra (= proche de la face du cube que nous ne pouvons pas voir) sont gros, les autres sont plus petits. Cela ressemble à la réalité !

Voici à quoi cela ressemble lorsque l’on est à « l’intérieur » du champ :

C’est l’image que vous obtenez ! C’est simplement un peu trop carré, donc une autre transformation mathématique est appliquée pour correspondre à la taille de la fenêtre :

Et c’est cette image qui est affichée !

Combiner des transformations : la matrice ModelViewProjection

… est une simple multiplication de matrices comme tu les aimes déjà :

// C++ : compute the matrix
glm::mat4 MVPmatrix = projection * view * model; // Remember : inverted !

// GLSL : apply it
transformed_vertex = MVP * in_vertex;

Mettre tout ensemble

• Première étape : générer la matrice ModelViewProjection (MVP). Cela doit être fait pour chaque modèle que vous affichez.

// Projection matrix : 45° Field of View, 4:3 ratio, display range : 0.1 unit <-> 100 units
glm::mat4 Projection = glm::perspective(glm::radians(45.0f), (float) width / (float)height, 0.1f, 100.0f);

// Or, for an ortho camera :
//glm::mat4 Projection = glm::ortho(-10.0f,10.0f,-10.0f,10.0f,0.0f,100.0f); // In world coordinates

// Camera matrix
glm::mat4 View = glm::lookAt(
               glm::vec3(4,3,3), // Camera is at (4,3,3), in World Space
               glm::vec3(0,0,0), // and looks at the origin
               glm::vec3(0,1,0)  // Head is up (set to 0,-1,0 to look upside-down)
               );

// Model matrix : an identity matrix (model will be at the origin)
glm::mat4 Model = glm::mat4(1.0f);
// Our ModelViewProjection : multiplication of our 3 matrices
glm::mat4 mvp = Projection * View * Model; // Remember, matrix multiplication is the other way around

• Seconde étape : passez les matrices au GLSL

// Get a handle for our "MVP" uniform
// Only during the initialisation
GLuint MatrixID = glGetUniformLocation(programID, "MVP");

// Send our transformation to the currently bound shader, in the "MVP" uniform
// This is done in the main loop since each model will have a different MVP matrix (At least for the M part)
glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &mvp[0][0]);

• Troisième étape : utiliser ça dans GLSL pour transformer nos sommets

// Input vertex data, different for all executions of this shader.
layout(location = 0) in vec3 vertexPosition_modelspace;

// Values that stay constant for the whole mesh.
uniform mat4 MVP;

void main(){

    // Output position of the vertex, in clip space : MVP * position
    gl_Position =  MVP * vec4(vertexPosition_modelspace,1);

}

• Fini ! Voici le triangle du deuxième tutoriel, toujours à l’origine (0, 0, 0), mais vu en perspective à partir du point (4, 3, 3), la tête en haut (0, 1, 0), avec un champ de vision de 45°.

Dans le sixième tutoriel tu vas apprendre à modifier ces valeurs dynamiquement à l’aide du clavier et de la souris pour créer une caméra comme dans les jeux, mais avant, tu dois apprendre comment donner quelques couleurs à nos modèles 3D (tutoriel 4) et des textures (tutoriel 5).

Exercices

• Essaye de changer la glm::perspective.
• Au lieu d’utiliser une projection en perspective, utilise une projection orthogonale (glm::ortho).
• Modifie la ModelMatrix pour déplacer, tourner et redimensionner le triangle.
• Faites la même chose, mais dans un ordre différent. Que remarques-tu ? Quel est le « meilleur » ordre que tu utiliserais pour un personnage ?

Addendum