• Normales
  • Normal de un triángulo
  • Normal de un vértice
  • Usando normales en OpenGL
• La parte difusa
  • La importancia de una normal a la superficie
  • Cuidado con el signo
  • Color del material
  • Modelando la luz
  • Uniendo todo
  • Hora de trabajar
  • Resultado
• El componente “ ambiente ”
  • Resultados
• El componente especular
  • Resultado final

En este octavo tutorial, vamos a aprender a hacer un shader. Esto incluye :

• Ser más brillante cuando se está cerca de una fuente de luz
• Tener reflejos de luz (Iluminación especular)
• Ser más oscuro cuando la luz no cae directamente sobre el modelo (Iluminación difusa)
• Hacer mucha trampa (Iluminación ambiental)

Esto NO incluye:

• Sombras. Este es un tema muy amplio y merece sus propios tutoriales.
• Reflejos de espejo (esto incluye el agua)
• Interacción de luz y materia muy complicada (como la cera)
• Materiales Anisotrópicos (Como metal raspado)
• Shading basado en física y realismo
• Oclusión ambiental (Es más oscuro en una cueva)
• Reflejo de color (un tapete rojo haría que una pared blanca se viera un poquito roja)
• Transparencias
• Cualquier clase de iluminación global (Es el nombre que se le da a todo lo anterior)

En una palabra: Básico.

Normales

En los últimos tutoriales, hemos estado hablando de normales y probablemente aún no entiendas qué son.

Normal de un triángulo

La normal de un plano es un vector de longitud 1 que es perpendicular a ese plano.

La normal de un triángulo es un vector de longitud 1 que es perpendicular a ese triángulo. Es fácilmente calculada encontrando el producto cruz de dos de sus lados (el producto cruz produce un vector perpendicular a A y B , recuerdas?) y normalizado : su longitud es 1. En pseudocódigo :

triangle ( v1, v2, v3 )
edge1 = v2-v1
edge2 = v3-v1
triangle.normal = cross(edge1, edge2).normalize()

No confundas normal con normalize(). Normalize() divide un vector (cualquier vector, no solo una normal) por su longitud para que dé como resultado 1. Normal es solamente el nombre que se le da a los vectores que representan, pues, una normal.

Normal de un vértice

Por extensión, llamamos normal de un vértice a la combinación de las normales de las caras triangulares que rodean al vértice. Esto se vuelve útil porque en los vertex shaders, lidiamos con vértices, no triángulos, así que es mejor tener información de un vértice. Además, en OpenGL no tenemos nunca información sobre triángulos. Aquí el pseudo código.

vertex v1, v2, v3, ....
triangle tr1, tr2, tr3 // all share vertex v1
v1.normal = normalize( tr1.normal + tr2.normal + tr3.normal )

Usando normales en OpenGL

Usar normales en OpenGL es muy fácil. Una normal es un atributo de un vértice, como lo es su posición, su color y sus coordenadas UV. Así que sólo hacemos lo usual. Nuestra función loadOBJ del tutorial 7 ya sabe traer esta información del archivo OBJ.

GLuint normalbuffer;
 glGenBuffers(1, &normalbuffer);
 glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
 glBufferData(GL_ARRAY_BUFFER, normals.size() * sizeof(glm::vec3), &normals[0], GL_STATIC_DRAW);

y

 // 3er buffer de atributos : normales
 glEnableVertexAttribArray(2);
 glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
 glVertexAttribPointer(
     2,                                // atributo
     3,                                // tamaño
     GL_FLOAT,                         // tipo
     GL_FALSE,                         // normalizado?
     0,                                
     (void*)0                          // desplazamiento del buffer 
 );

y esto es suficiente para empezar.

La parte difusa

La importancia de una normal a la superficie

Cuando la luz toca un objeto, una gran parte de ella es reflejada en todas las direcciónes. Este es el “componente difuso”. Ya veremos qué pasa con el resto de la luz.

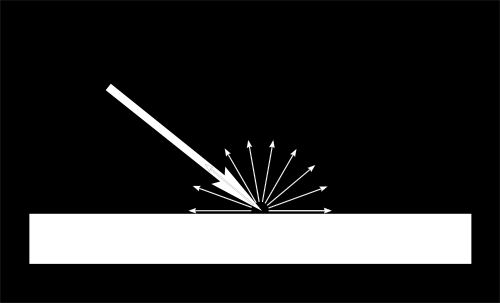
Cuando un cierto flujo de luz llega a la superficie es iluminada de forma diferente de acuerdo al ángulo de incidencia.

Si la luz es perpendicular a la cara, se concentra en una pequeña superficie, si llega en un ángulo, la misma cantidad se esparce por una mayor superficie :

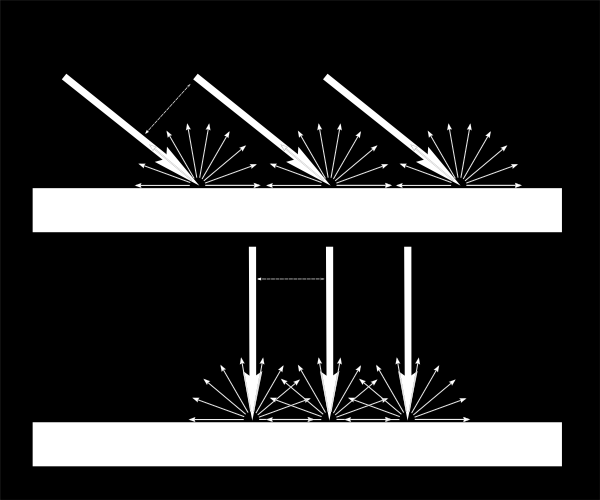
Esto significa que cada punto de la superficie se verá más oscuro con la luz en ángulo (pero recuerda, más puntos serán iluminados, la cantidad de luz es la misma en total).

Esto significa que cuando calculamos el color de un pixel, el ángulo entre la luz entrante y la normal de la superficie importan, y mucho, resultando :

// Coseno del ángulo entre la normal y la dirección de la luz ,
// restringido a mayor que 0
//  - la luz está en la vertical del triángulo -> 1
//  - la luz es perpendicular al triángulo -> 0
float cosTheta = dot( n,l );

color = LightColor * cosTheta;

En este código, n es la normal y I es el vector unitario que va de la superficie hacia la luz (y no al contrario. Pueda que no sea intuitivo pero las matemáticas son más fáciles).

Cuidado con el signo

Falta algo en nuestra fórmula de coseno de teta. Si la luz está detrás del triángulo, n y I seràn opuestos así que n.I será negativo. Esto significa que el color resultará un número negativo. Por eso limitamos la función a todo lo que es mayor que 0 :

// Coseno del ángulo entre la normal y la dirección de la luz ,
// restringido a mayor que 0
//  - la luz está en la vertical del triángulo -> 1
//  - la luz es perpendicular al triángulo -> 0
//  - la luz está detrás del triángulo -> 0
float cosTheta = clamp( dot( n,l ), 0,1 );

color = LightColor * cosTheta;

Color del material

Por supuesto que el color de salida depende del color del material. En esta imagen, la luz blanca está hecha de verde rojo y azul. Cuando toca material rojo, la luz verde y azul son absorbidas reflejando solo el rojo.

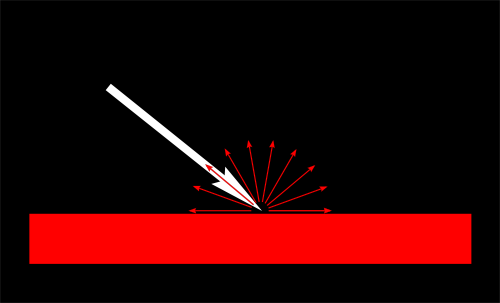
Podemos modelar esto con una multiplicación simple :

color = MaterialDiffuseColor * LightColor * cosTheta;

Modelando la luz

Primero asumiremos que tenemos una luz puntual que emite luz en todas las direcciónes en el espacio, como una vela.

Con esa luz, el flujo que nuestra superficie recibe depende de la distancia de la luz al objeto. Entre más lejos, menos luz. De hecho, la cantidad de luz decrece con el cuadrado de la distancia :

color = MaterialDiffuseColor * LightColor * cosTheta / (distance*distance);

Por último, necesitamos otro parámetro para controla la potencia de la luz. Esto se puede hacer con LightColor (y lo haremos en otro tutorial), por ahora vamos a tener un color (por ejemplo blanco) y una potencia (ejemplo 60 Watts).

color = MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance);

Uniendo todo

Para que este código funcione, necesitamos varios parámetros (varios colores y potencias) y más código.

MaterialDiffuseColor trae de la textura.

LightColor y LightPower se agregan al shader a través de uniforms de GLSL.

cosTheta depende de n y l. Podemos expresarlos en cualquier espacio que sea el mismo para los dos. Escogemos el espacio de cámara porque es más fácil calcular la posición de la luz en este espacio :

// La normal del fragmento en espacio de la cámara.
 vec3 n = normalize( Normal_cameraspace );
 // Dirección de la luz (del fragmento hacia la luz)
 vec3 l = normalize( LightDirection_cameraspace );

Con Normal_cameraspace y LightDirection_cameraspace calculados en el the Vertex shader y enviados al fragment shader :

// Posición de salida del vértice : MVP * position
gl_Position =  MVP * vec4(vertexPosition_modelspace,1);

// Posición del vértice en el mundo : M * position
Position_worldspace = (M * vec4(vertexPosition_modelspace,1)).xyz;

// Vector que va del vértice a la cámara, en el espacio de cámara.
// En el espaci de la cámara, la cámara está en el origen (0,0,0).
vec3 vertexPosition_cameraspace = ( V * M * vec4(vertexPosition_modelspace,1)).xyz;
EyeDirection_cameraspace = vec3(0,0,0) - vertexPosition_cameraspace;

// Vector que va del vértice a la luz, en espacio de cámara. Se omite M por que es la identidad.
vec3 LightPosition_cameraspace = ( V * vec4(LightPosition_worldspace,1)).xyz;
LightDirection_cameraspace = LightPosition_cameraspace + EyeDirection_cameraspace;

// Normal del vértice en espacio de cámara
Normal_cameraspace = ( V * M * vec4(vertexNormal_modelspace,0)).xyz; // Solo es correcto si  ModelMatrix no escala el modelo ! De lo contrario use su transpuestá inversa

Este código puede parecer impresionante, pero no es nada que no hayamos aprendido en el tutorial 3 : Matrices. Yo me tomé la molestia de poner el nombre del espacio en el que está cada vector para que puedas seguir el proceso de transformaciones. ** Ponle mucha atención. **

M y V son las matrices Modelo y Vista, que son enviadas al shader de la misma forma que MVP.

Hora de trabajar

En este momento sabes todo lo que necesitas saber para hacer el código de una iluminación difusa. Ve y aprende de la forma difícil ;)

Resultado

Solo con el componente difuso tenemos el siguiente resultado (disculpa la textura fea nuevamente) :

Se ve mejor que antes, pero aún falta mucho. En particular, la parte de atrás de Suzanne es completamente negra, ya que usamos clamp().

El componente “ ambiente ”

El componente de ambiente es una de las trampas más grandes.

Estamos esperando que la parte de atrás de Suzanne reciba más luz porque en la vida real, la lámpara alumbra la pared de atrás que a su vez ilumina (levemente) la parte de atrás del objeto

Pero eso toma mucho poder computacional.

Así que vamos a crear una luz falsa. De hecho simplemente hace que el modelo 3D *emita *luz para que no aparezca completamente negro.

Se puede hacer así :

vec3 MaterialAmbientColor = vec3(0.1,0.1,0.1) * MaterialDiffuseColor;

color =
 // Ambiente : simulates luz indirecta
 MaterialAmbientColor +
 // Diffuse : "color" of the object
 MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) ;

Veamos en qué resulta

Resultados

Ok, se ve un poco mejor. Puedes ajustar el (0.1, 0.1, 0.1) si quieres mejores resultados.

El componente especular

La otra parte de la luz es reflejada en la dirección del ángulo saliente del ángulo en que la luz toca la superficie. Esto se denomina componente especular.

Como puedes ver en la imagen, se forma algo como un círculo de reflejo. En casos extremos el componente puede ser nulo, lo que resulta en que el reflejo es muy pequeño y brillante (porque toda la luz se refleja en una sola dirección) y obtienes un espejo.

(Podemos variar los parámetros para obtener un espejo, pero en nuestro caso , lo único que debemos tener en cuenta en este espejo es la lámpara, lo que haría un espejo muy raro

// Vector del ojo (hacia la cámara)
vec3 E = normalize(EyeDirection_cameraspace);
// Dirección en la que el triángulo refleja la luz
vec3 R = reflect(-l,n);
// Coseno del ángulo entre la normal y la dirección de la luz ,
// restringido a mayor que 0
//  - la luz está en la vertical del triángulo -> 1
//  - la luz es perpendicular al triángulo -> 0
float cosAlpha = clamp( dot( E,R ), 0,1 );

color =
    // Ambiente : Simula la luz indirecta
    MaterialAmbientColor +
    // Difuso : El "color" del objeto
    MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) ;
    // Especular : Reflejo resaltado, como un espejo
    MaterialSpecularColor * LightColor * LightPower * pow(cosAlpha,5) / (distance*distance);

R es la dirección en la que la luz se refleja. E es el inverso de la dirección del ojo (así como lo hicimos para “l”). Si el ángulo entre estos dos es pequeño significa que estamos viendo directo al reflejo.

pow(cosAlpha,5) se usa para controlar el ancho del reflejo especular, aumenta en 5 para obtener un reflejo más pequeño.

Resultado final

Nota los reflejos especulares resaltados en la nariz y las cejas.

Este modelo de shading se ha usado durante años debido a su simplicidad. Tiene bastantes problemas, por eso se reemplaza por modelos basados en física como microfacetas BRDF, pero eso lo veremos luego.

En el siguiente tutorial vamos a mejorar el rendimiento de tu VBO. Será el inmediatamente siguiente !