Tutorial 6 : Teclado y ratón
Bienvenidos a nuestro sexto tutorial !
Aquí aprenderemos como usar el ratón y el teclado para mover la cámara justo como un juego de disparos en primera persona.
La Interfaz
Dado que este código será reutilizado a través de distintos tutoriales de aquí en adelante, lo pondremos en un archivo separado: common/controls.cpp, y declararemos la función en common/controls.hpp para que tutorial06.cpp sepa del código.
El código de tutorial06.cpp no es muy diferente de nuestro anterior tutorial. La modificación más grande presente es que en lugar de calcular la matriz de Modelo Vista Proyección una vez, lo haremos en cada cuadro. Así que pongamos este código en el ciclo principal de la aplicación:
do{
// ...
// Compute the MVP matrix from keyboard and mouse input
computeMatricesFromInputs();
glm::mat4 ProjectionMatrix = getProjectionMatrix();
glm::mat4 ViewMatrix = getViewMatrix();
glm::mat4 ModelMatrix = glm::mat4(1.0);
glm::mat4 MVP = ProjectionMatrix * ViewMatrix * ModelMatrix;
// ...
}
Este código necesita 3 nuevas funciones :
- computeMatricesFromInputs() que lee las entradas del teclado y el ratón y calcula las matrices de la Vista y la Proyección. Aquí es en donde toda la magia tiene lugar.
- getProjectionMatrix() retorna la matriz de Proyección calculada.
- getViewMatrix() retorna la matriz de Vista calculada.
Esta es sólo una de las formas para hacerlo, claro está. Si no te gusta la manera en cómo están implementadas estas funciones, cámbialas con completa libertad.
Veamos ahora que hay dentro de controls.cpp.
The actual code
We’ll need a few variables.
// position
glm::vec3 position = glm::vec3( 0, 0, 5 );
// horizontal angle : toward -Z
float horizontalAngle = 3.14f;
// vertical angle : 0, look at the horizon
float verticalAngle = 0.0f;
// Initial Field of View
float initialFoV = 45.0f;
float speed = 3.0f; // 3 units / second
float mouseSpeed = 0.005f;
FoV es el nivel de acercamiento. 80° = ángulo muy amplio, con enormes deformaciones. 60° - 45° : estándar. 20° : gran acercamiento.
Lo primero que haremos es recalcular position, horizontalAngle, verticalAngle y FoV a partir de las entradas y luego evaluaremos las matrices de Vista y Proyección a partir de dichas variables.
Orientación
Leer la posición del ratón es fácil:
// Get mouse position
int xpos, ypos;
glfwGetMousePos(&xpos, &ypos);
but we have to take care to put the cursor back to the center of the screen, or it will soon go outside the window and you won’t be able to move anymore.
// Reset mouse position for next frame
glfwSetMousePos(1024/2, 768/2);
Observa que este código asume que la ventana de la aplicación es de 1024*768, lo cual no podría no ser en el caso en tu aplicación. Puedes usar glfwGetWindowSize si quieres.
Vamos ahora a calcular los ángulos de visión :
// Compute new orientation
horizontalAngle += mouseSpeed * deltaTime * float(1024/2 - xpos );
verticalAngle += mouseSpeed * deltaTime * float( 768/2 - ypos );
Leamos esto de derecha a izquierda :
- 1024/2 - xpos indica que tan lejos está el ratón del centro de la ventana. Entre más grande sea este valor, más querremos girar.
- float(…) convierte esta posición en un número de punto flotante para que podamos multiplicarlo sin problemas.
- mouseSpeed sirve para acelerar o ralentizar las rotaciones. Ajusta esto según tu gusto o mejor aún, deja que el usuario lo haga.
- += : Si no mueves el ratón, 1024/2-xpos será igual a 0, y horizontalAngle+=0 no cambia la variable horizontalAngle. Si en lugar de esto tuvieses un “=”, te verías forzado a regresar a la orientación original con cada cuadro, lo cual no es bueno.
Podemos ahora calcular un vector que representa, en Coordenadas del Mundo, la dirección en la que estamos mirando.
// Direction : Spherical coordinates to Cartesian coordinates conversión
glm::vec3 direction(
cos(verticalAngle) * sin(horizontalAngle),
sin(verticalAngle),
cos(verticalAngle) * cos(horizontalAngle)
);
Éste es un cálculo básico, pero si no sabes qué es un coseno o un seno, dale clic al siguiente link para obtener una corta explicación:
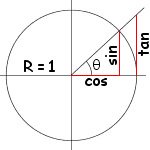
La fórmula arriba es tan sólo una generalización para tres dimensiones.
Ahora queremos calcular el vector “arriba” de manera confiable. Observa que “arriba” no está siempre apuntando en la dirección +Y : si miras hacia abajo, por ejemplo, el vector “arriba” estará en posición horizontal. Aquí hay un ejemplo de cámera con la misma posición, el mismo objetivo, pero diferente vector “arriba”.
En nuestro caso, la única constante es que el vector que va hacia la derecha de la cámara será siempre horizontal. Puedes verificar esto poniendo tu brazo en posición horizontal, mirando hacia arriba, abajo y en cualquier dirección. Definamos entonces nuestro vector “derecho”: Sus coordenada en Y es 0 ya que siempre será horizontal. Sus coordenadas X y Z son las que se muestran en la figura más abajo, pero con los ángulos rotados 90°, o Pi/2 radianes.
// Right vector
glm::vec3 right = glm::vec3(
sin(horizontalAngle - 3.14f/2.0f),
0,
cos(horizontalAngle - 3.14f/2.0f)
);
Tenemos entonces un vector “derecho” y una “dirección” o vector “frontal”. El vector “arriba” es un vector que es perpendicular a estos dos. Existe una herramienta matemática que nos facilita éste calculo: El producto cruz:
// Up vector : perpendicular to both direction and right
glm::vec3 up = glm::cross( right, direction );
En resumen, lo que hace el producto cruz es muy simple: Recuerda la Regla de la Mano Derecha del Tutorial 3: El primer vector es el pulgar, el segundo es el dedo índice y el tercero es el dedo corazón. Esta astucia es bastante útil para que recordemos cómo funciona éste cálculo.
Posición
El código es bastante directo. Por cierto, Por cierto, aquí usamos las teclas de las flechas arriba/abajo/derecha en lugar de AWSD dado que en mi teclado, AWSD es en realidad ZQSD, al igual que los teclado QUERZ, eso sin mencionar los teclados coreanos. No tengo idea de cómo son los teclados coreanos, pero voy a suponer que también son diferentes.
// Move forward
if (glfwGetKey( GLFW_KEY_UP ) == GLFW_PRESS){
position += direction * deltaTime * speed;
}
// Move backward
if (glfwGetKey( GLFW_KEY_DOWN ) == GLFW_PRESS){
position -= direction * deltaTime * speed;
}
// Strafe right
if (glfwGetKey( GLFW_KEY_RIGHT ) == GLFW_PRESS){
position += right * deltaTime * speed;
}
// Strafe left
if (glfwGetKey( GLFW_KEY_LEFT ) == GLFW_PRESS){
position -= right * deltaTime * speed;
}
El único elemento especial aquí es la variable deltaTime. No vas a querer moverte en una unidad para cada cuadro por una simple razón :
- Si tienes un computador rápido y corre la aplicación a 60 cuadros por segundo, te moverás a 60*speed unidades en 1 segundo.
- Si tienes un computador lento y corre la aplicación a 20 cuadros por segundo, te moverás el equivalente a 20*speed unidades en 1 segundo.
Dado que tener un mejor computador no es una excusa para ir más rápido, tienes que ajustar la distancia a una escala diferente, definida por el “tiempo desde el último del cuadro” o “deltaTime”.
- Si tienes un computador rápido y corre la aplicación a 60 cuadros por segundo, te moverás a 1/60 * speed unidades en 1 cuadro, es decir 1*speed en 1 segundo.
- Si tienes un computador lento y corre la aplicación a 20 cuadros por segundo, te moverás a 1/20 * speed unidades en 1 cuadro, es decir 1*speed en 1 segundo.
Lo cual es mucho mejor. deltaTime es bastante sencillo de calcular :
double currentTime = glfwGetTime();
float deltaTime = float(currentTime - lastTime);
Campo de Visión
Sólo por diversión, vamos a ligar la rueda del ratón al Campo de Visión, para obtener una manera simple de hacer zoom:
float FoV = initialFoV - 5 * glfwGetMouseWheel();
Calculando las matrices
Con todo lo que hemos hecho, hallar las matrices es bastante directo. Usaremos exactamente las mismas funciones que antes, pero con nuestros nuevos parámetros.
// Projection matrix : 45° Field of View, 4:3 ratio, display range : 0.1 unit <-> 100 units
ProjectionMatrix = glm::perspective(glm::radians(FoV), 4.0f / 3.0f, 0.1f, 100.0f);
// Camera matrix
ViewMatrix = glm::lookAt(
position, // La cámara está aquí
position+direction, // y mira aquí. En posición más dirección
up // La cámara mira hacia arriba (pon 0,-1,0 para mirar cabeza abajo)
);
Resultados

Backface Culling (Ocultación de las caras posteriores)
Ahora que puedes moverte libremente alrededor, puedes darte cuenta que si vas dentro del cubo, los polígonos aún se muestran. Esto puedo parecer obvio, pero darse cuenta de esto nos da la oportunidad de optimizar nuestra aplicación. De hecho, en una aplicación tradicional, nunca deberías estar dentro del cubo.
La idea es dejar que la GPU verifique si la cámara está detrás o enfrente de un triángulo. Si está en frente, se muestra el triángulo, si está detrás y la malla es cerrada y no estamos dentro de la mallo, entonces habrá otro triángulo enfrente de ella y nadie se dará cuenta de nada excepto que todo irá más rápido: pintaremos en promedio dos veces menos triángulos!
Lo mejor de todo, es que verificar esto es muy fácil. La GPU calcula el vector normal de un triángulo (usando el producto cruz, ¿recuerdas?) y verifica si dicha normal apunta hacia la cámara o no.
Desafortunadamente, esto tiene un costo: La orientación del triángulo es implícita. Esto significa que si inviertes dos vértices en tu buffer, probablemente terminarás con un agujero en donde no debería haberlo. Sin embargo, y por lo general, el esfuerzo adicional vale la pena. A menudo, puedes sólo hacer clic en “invertir normales” en tu herramienta de modelado 3D (lo cual invertirá los vértices y con ellos, las normales) y todo se arreglará.
Habilitando backface culling en un abrir y cerrar de ojos:
// Cull triangles which normal is not towards the camera
glEnable(GL_CULL_FACE);
Ejercicios
- Restringe verticalAngle de tal manera que la cámara no pueda quedar de cabeza
- Crea una cámara que gire alrededor de un objeto en particular ( position = ObjectCenter + ( radius * cos(time), height, radius * sin(time) ) ); liga el radio/altura/tiempo al teclado o al ratón o lo que quieras.
- Diviértete !