• Coordenadas homogéneas
• Transformación de matrices
  • Introduction a las matrices
  • Matrices de traslación\
  • La matriz identidad
  • Escalando matrices
  • Rotación de matrices
  • Acumulando transformaciones
• Matrices modelo, vista y proyección
  • La matriz modelo
  • La matriz vista
  • La matriz proyección
  • Acumulando transformaciones : La matriz ModeloVistaProyección
• Uniendo todo
• Ejercicios

Los motores no mueven la nave. La nave permanece en su lugar y el universo se mueve alrededor de ella.

Futurama

Este es el tutorial más importante de los tutoriales de principiante. Leelo al menos 8 veces.

Coordenadas homogéneas

Hasta ahora, consideramos las coordenadas 3D como triplas (x,y,z). Vamos a introducir a ‘w’. Ahora tendremos vectores (x,y,z,w).

Será más sencillo después, por ahora solo recuerda que:

• Si w==1 el vector es una posición en el espacio.
• Si w==0 el vector e suna dirección.

(Recuerdelo para siempre)

¿Qué diferencia hace? Bueno, para una rotación no hace la diferencia. Cuando usted rota un punto o una dirección, obtiene el mismo resultado. Sin embargo para una traslación (mover un punto en una dirección), las cosas son diferentes. Que podria significar “traslación de una dirección”? Nada.

Las coordenadas homogéneas usan una única fórmula matemática para lidiar con estos dos casos cases.

Transformación de matrices

Introduction a las matrices

En términos simples, una matriz es un arreglo de números con un número predefinido de filas y columnas. Por ejemplo, una matriz de 2x3 se ve así

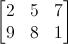
En computación gráfica se usan matrices de 4x4. Estas matrices nos permitirán transformar nuestros vértices (x,y,z,w).

Esto se hace multiplicando el vértice con la matriz :

Matrix x Vertex (in this order !!) = TransformedVertex

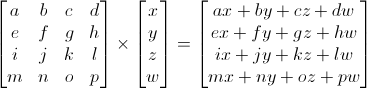
No es tan terrible como se ve. Pon tu dedo izquierdo sobre la a y tu dedo derecho sobre la x. Esto es ax_. Mueve tu dedo izquierdo al siguiente número (b), y tu dedo derecho a (y). ahora tienes by. Una vez más, cz. Una vez más : dw. ax + by + cz + dw. Tienes tu nueva x ! haz lo mismo para cada línea y obtendrás tu vector (x,y,z,w).

Esto es aburrido de calcular, y lo haremos frecuentemente, así que mejor digamosle al computador que lo haga en nuestro lugar.

En C++, con GLM:

glm::mat4 myMatrix;
glm::vec4 myVector;
// Llene  myMatrix y myVector de alguna forma
glm::vec4 transformedVector = myMatrix * myVector; // En este orden, es importante.

En GLSL :

mat4 myMatrix;
vec4 myVector;
// Llene  myMatrix y myVector de alguna forma
vec4 transformedVector = myMatrix * myVector; // Si basicamente es lo mismo que GLM

( ¿Ya copiaste y pegaste el código? intentalo )

Matrices de traslación\

Estas son las matrices más fáciles de entender. Una matriz de traslación se ve así :

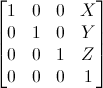
Donde X,Y,Z son los valores de tu posición.

Así que si queremos trasladar el vector (10,10,10,1) 10 unidades en la dirección X, obtendremos :

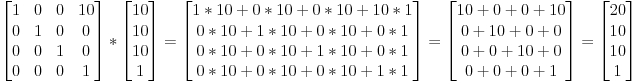
(Intentalo! Inteeeeentalo)

… obtendremos un vector homogéneo (20,10,10,1) ! Recuerda el 1 significa que es una posición no una dirección. La transformación no ha cambiado eso, lo cual es bueno.

Ahora veremos lo que le pasa a un vector dirección en dirección -z : (0,0,-1,0)

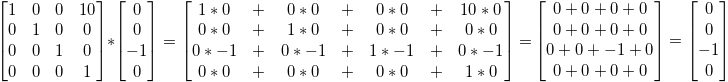
… es decir nuestra dirección original (0,0,-1,0), lo cual es genial porque como te dije antes, mover una dirección no tiene sentido.

¿Cómo se traduce esto a código?

En C++, con GLM:

#include <glm/gtx/transform.hpp> // after <glm/glm.hpp>
 
glm::mat4 myMatrix = glm::translate(glm::mat4(), glm::vec3(10.0f, 0.0f, 0.0f));
glm::vec4 myVector(10.0f, 10.0f, 10.0f, 0.0f);
glm::vec4 transformedVector = myMatrix * myVector; // guess the result

En GLSL :

vec4 transformedVector = myMatrix * myVector;

De hecho casi nunca se hace esto en GLSL. La mayoría de las veces se usa glm::translate() en C++ para calcular la matriz, enviarla a GLSL y solo hacer la multiplicación.

La matriz identidad

Esta es especial. No hace nada. Pero la menciono porque es importante sabe que al multiplicar A por 1.0 te da 1.

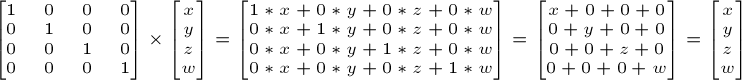
En C++ :

glm::mat4 myIdentityMatrix = glm::mat4(1.0f);

Escalando matrices

Escalar es muy facil tambien :

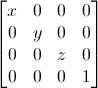
Así que si quieres escalar un vector (posición o dirección, no importa) por 2.0 en todas las direcciones :

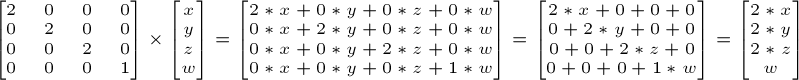
Y la w no cambia. Te preguntaras cual es el significado de “escalar una dirección”? Pues, con frecuencia no significa mucho, pero a veces resulta útil.

(Nota que la matriz identidad es solo un caso especial de escalamiento de matrices con (X,Y,Z) = (1,1,1). También es un caso especial, la translación con una matriz (X,Y,Z)=(0,0,0) )

En C++ :

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 myScalingMatrix = glm::scale(2.0f, 2.0f ,2.0f);

Rotación de matrices

Estas son un poco más complicadas. Omitiré detalles por simplicidad. Para más información mira Matrices and Quaternions FAQ (recurso popular en varios idiomas). Y puedes mirar también los Rotations tutorials

En C++ :

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::vec3 myRotationAxis( ??, ??, ??);
glm::rotate( angle_in_degrees, myRotationAxis );

Acumulando transformaciones

Ya sabemos rotar , trasladar y escalar nuestros vectores. Seria genial combinar todas estas transformaciones. Esto se hace multiplicando las matrices, por ejemplo :

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;

!!! ATENCIÓN !!! Estas líneas primero hacen el ESCALAMIENTO, luego la ROTACIÓN y luego la TRANSLACIÓN. Así es como funciona la multiplicación.

Escribir las operaciones en otro orden no produce el mismo resultado. Intentalo tu mismo :

• Da un paso adelante (cuidado con tu computador) y voltea a la derecha.

• Voltea a la derecha y da un paso al frente.

De hecho, el orden de arriba es el que usualmente necesitarás para personajes de un juego y otros elementos : Escalas primero si es necesario, luego escoges una dirección y luego trasladas. Eliminemos rotación por simplicidad. Por ejemplo, dado un modelo de un barco :

• La forma incorrect :
  • Trasladar el barco en (10,0,0). Su centro está ahora a 10 unidades del origen.
  • Escalar el barco por 2. Cada coordenada es multiplicada por 2 con relación al origen, que ya está lejos de aquí.. Así que vas a terminar con un barco grande pero centrado en 2*10 = 20. Y no quieres eso.
• La forma correcta :
  • Escalar tu barco por 2. Tienes un gran barco centrado en el origen.
  • Trasladas tu barco. Tendrá el tamaño y la posición adecuada.

La multiplicación matriz-matriz es muy similar a la multiplicación matriz-vector, así que vamos a saltarnos esa parte y si tienes dudas consulta las preguntas frecuentes de Matrices y cuaterniones. Por ahora le diremos al computador que lo haga por nosotros :

En C++, con GLM :

glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;

En GLSL :

mat4 transform = mat2 * mat1;
vec4 out_vec = transform * in_vec;

Matrices modelo, vista y proyección

Para el resto del tutorial, vamos a suponer que todos conocen el famosísimo mono de Blender : El mono Suzanne.

Las matrices modelo, vista y proyección, son muy útiles para hacer las transformaciones limpiamente. Pueda que nunca uses esto (ya lo hicimos en los tutoriales 1 y 2). Pero deberías. Es como todos lo hacen, porque es la forma más fácil.

La matriz modelo

Este modelo, como nuestro triángulo querido, está definido por un set de vértices. Las coordenadas (x,y,z) de estos vértices, son definidas relativamente a un centro : un lugar llamado (0,0,0), es el centro del objeto.

Queremos poder mover este objeto, por ejemplo controlandolo con el teclado o el mouse. Ya sabes hacerlo, es facil : translacion*rotacion*escala y listo. Aplicas está matriz a todos tus vértices en cada cuadro (en GLSL, no en C++!) y todo se mueve. Algo que no se mueve está en el centro del mundo.

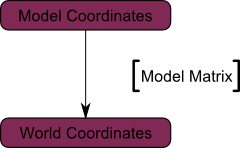
Al hacer esto tus vértices están en el espacio de mundo. Este es el significado de la flecha negra de la imagen abajo : Fuimos del espacio del modelo (todos los vértices están definidos con respecto centro del modelo) al espacio del mundo (all vértices defined relatively to the center of the world).

Podemos verlo todo en el siguiente diagrama :

La matriz vista

Vamos a citar a “Futurama” otra vez:

El motor no mueve la nave. La nave se queda donde está y los motores mueven el universo a su alrededor.

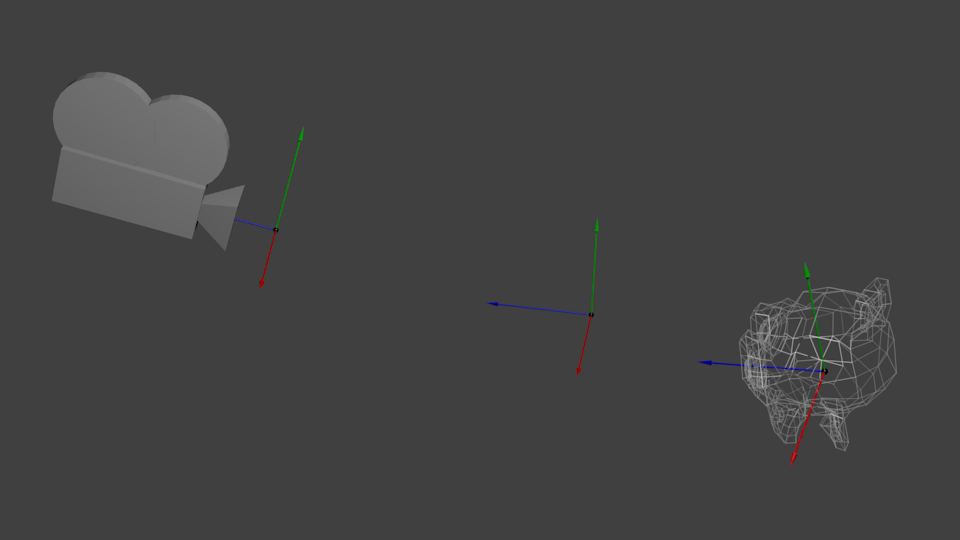
Cuando lo piensas, esto se aplica a las cámaras. Si quieres ver una montaña desde otro ángulo, puedes mover la cámara… o mover la montaña. No es práctico en la vida real, es solo que así es más fácil en computación gráfica.

Inicialmente, la cámara está en el origen del espacio mundo. Para mover el mundo, simplemente se introduce otra matriz. Digamos que quieres mover tu cámara 3 unidades a la derecha (+X). Esto es equivalente a mover todo el mundo (y lo que contenga) 3 unidades a la izquierda !. Mientras tu cerebro se derrite, vamos a hacerlo :

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 ViewMatrix = glm::translate(glm::mat4(), glm::vec3(-3.0f, 0.0f ,0.0f));

Una vez más, la imagen abajo ilustra esto : Fuimos del espacio mundo (todos los vértices están definidos relativamente al centro del mundo) al espacio cámara (todos los vértices se definen relativamente a la cámara).

Antes que tu cabeza explote con todo esto, disfruta la gran función de GLM : glm::lookAt :

glm::mat4 CameraMatrix = glm::lookAt(
    cameraPosition, // La posición de tu cámara en el espacio mundo
    cameraTarget,   // Hacia donde quieres mirar, en el espacio mundo
    upVector        // Probablemente glm::vec3(0,1,0), porque (0,-1,0) te haría mirar cabeza abajo, aunque puede ser divertido.
);

Aquí está el diagrama obligatorio :

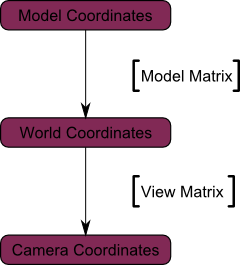
Pero aún no hemos acabado.

La matriz proyección

Ahora estamos en el espacio cámara. Esto significa que después de todas las transformaciones, un vértice que tenga coordenadas x==0 y y==0 debe pintarse en el centro de la pantalla. Pero no solo usamos las coordenadas x y y para determinar la posición de un objeto en la pantalla : su distancia a la cámara (z) también cuenta ! Para dos vértices con las mismas coordenadas x y y, el vértice con mayor (z) estará más en el centro de la pantalla que el otro.

Esto es lo que se llama una perspectiva de proyección :

Y por suerte para nosotros, una matriz 4x4 puede representar está proyección [^projection] :

// Genera una matriz difícil de leer pero al menos es 4x4
glm::mat4 projectionMatrix = glm::perspective(
    glm::radians(FoV), // El campo de visión vertical, en radián: la cantidad de "zoom". Piensa en el lente de la cámara. Usualmente está entre 90° (extra ancho) y 30° (zoom aumentado)
    4.0f / 3.0f,       // Proporción. Depende del tamaño de tu ventana 4/3 == 800/600 == 1280/960, Parece familiar?
    0.1f,              // Plano de corte cercano. Tan grande como sea posible o tendrás problemas de precisión.
    100.0f             // Plano de corte lejano. Tan pequeño como se pueda.
);

Una última vez :

Fuimos del espacio de la cámara (todos los vértices definidos relativamente a la cámara) al espacio homogéneo (todos los vértices definidos en un pequeño cubo. Todo aquello que está dentro del cubo está dentro de la pantalla).

Y el diagrama final :

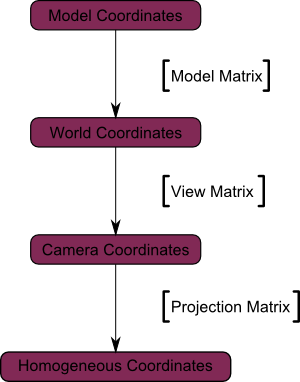
Aquí hay otro diagrama para que entiendas mejor lo que pasa con todo esto de la proyección. Antes de la proyección, tenemos nuestros objetos azules, en el espacio de la cámara, y la forma roja representa la pirámide de la cámara : la parte de la escena que la cámara ve en efecto.

Multiplicar todo por la matriz de proyección tiene el siguiente efecto :

En está imagen el cono es ahora un cubo perfecto (entre -1 y 1 en todos los ejes, es un poco difícil de entender), y todos los objetos azules ahora parecen deformados de algún modo. Los objetos cercanos a la cámara (cerca de la cara del cubo de -1 a 1) son más grandes, los otros son más pequeños. Tal como en la vida real.

Veamos ahora como se ve por “detrás” de la piramide :

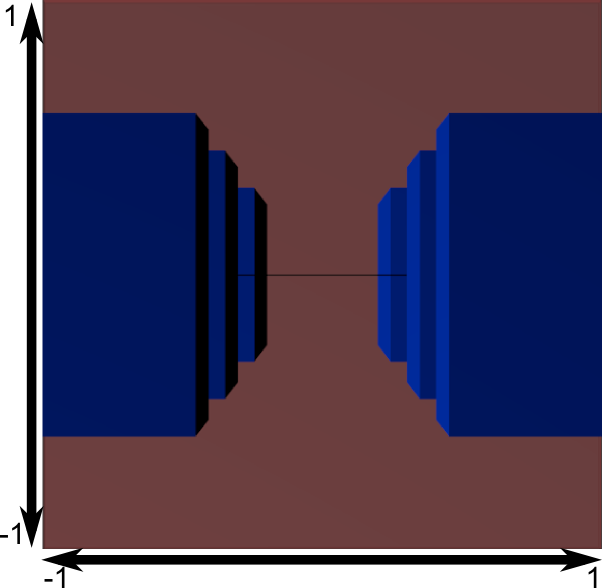
He aquí tu imagen ! Es un poco cuadrada, así que otra transformación matemática es aplicada (es automatica, no tienes que hacerla en el shader) para quedar del tamaño de la pantalla correctamente.

Y está imagen de hecho es el render !

Acumulando transformaciones : La matriz ModeloVistaProyección

… Solo una multiplicación estándar, así como te gustan !

// C++ : calcular la matriz
glm::mat4 MVPmatrix = projection * view * model; // Recurda : invertida !

// GLSL : aplicala
transformed_vertex = MVP * in_vertex;

Uniendo todo

• Primer paso : generar la matriz MVP. Esto se hace para cada modelo que se renderice.
• Segundo paso : entregarle todo a GLSL.
• Tercer paso : usar GLSL para transformar nuestros vértices.
• Listo ! He aquí el mismo triángulo del tutorial 2, aún en el origen (0,0,0), pero visto desde la perspectiva del punto (4,3,3), cabeza arriba (0,1,0), con un campo de visión de 45°.

En el tutorial 6 aprenderás a modificar estos valores de forma dinámica usando el teclado y el mouse para crear una cámara como de los juegos. Pero primero, vamos a aprender a darle un color a nuestros modelos 3D (tutorial 4) y usar texturas (tutorial 5).

Ejercicios

• Intenta cambiar la glm::perspective.
• En lugar de usar una perspectiva de proyección, usa una proyección ortográfica (glm::ortho).
• Modifica la matriz de modelo para trasladar, rotar y luego escalar el triángulo.
• Haz lo mismo en diferentes órdenes. Qué notas? cual es el “mejor” orden que se debe usar para un personaje?

Addendum